Comprendre la loi des gaz parfaits par la mécanique des molécules

Supposons pour simplifier qu’une molécule rebondisse sur la paroi de droite à la vitesse u orientée perpendiculairement à la paroi. A chaque rebond elle perd la quantité de mouvement 2 m u (lire article « Les lois de la dynamique » ) qu’elle communique donc à la paroi. D’après la loi de la dynamique de Newton, la force sur la paroi est égale à la quantité de mouvement ainsi reçue par unité de temps. Celle-ci est obtenue en multipliant cette quantité de mouvement élémentaire par le nombre de collisions par unité de temps. Ce nombre est proportionnel au nombre de molécules par unité de volume, soit N/V, où N est le nombre total de molécules et V le volume total du fluide. En un temps dt, seules vont atteindre la paroi les molécules présentes dans une tranche d’épaisseur u dt, soit un volume S u dt où S est la surface de paroi considérée (voir Figure). En fait seule la moitié de ces molécules le feront, celles qui se déplacent vers la droite, soit un nombre ½ (N/V) S u dt. Le nombre de chocs par unité de temps est donc ½ (N/V) S u.

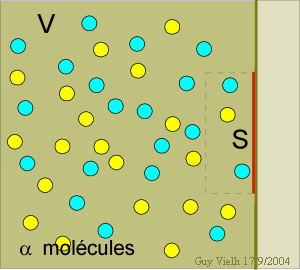
En multipliant par la quantité de mouvement 2 m u apportée par chaque molécule et en divisant par la  surface, on obtient ainsi la pression p = (N/V) mu².

La vitesse u de chaque molécule dépend du hasard des chocs qu’elle subit. La pression résulte de la moyenne de u²  sur toutes les molécules, notée <u²>. La formule précédente donne donc  pV = Nm<u²>. La comparaison avec la loi des gaz parfaits permet ainsi de relier l’énergie cinétique des molécules (1/2)m<u²> à la température par (1/2)m<u²> = (1/2)k_BT.

Les molécules se déplacent en fait avec un vecteur vitesse u dans toutes les directions, et selon le théorème de Pythagore, u² = u²+v²+w², ou u, v, w sont les projections des vitesses selon chaque coordonnée. Celles-ci sont identiques en moyenne dans toutes les directions, <u²>=<u²>+<v²>+<w²>=3<u²>, ce qui permet d’exprimer l’énergie cinétique totale de translation des molécules comme  (1/2)m<u²> = (3/2)k_BT.

Les chocs sur la paroi ne sont pas élastiques comme nous l’avons supposé ici : les molécules échangent de l’énergie avec les atomes de la paroi. Cependant à l’équilibre thermique, il n’y a pas d’échange net d’énergie entre le gaz et la paroi, ce qui valide l’hypothèse d’un choc élastique en moyenne. De même les molécules n’échangent pas en moyenne de quantité de mouvement tangentiellement à la paroi, car leur vitesse le long de la paroi est nulle en moyenne. Il n’y a donc pas de force tangentielle. Il n’en serait plus de même en présence d’un écoulement le long de la paroi qui s’accompagne d’une force tangentielle de viscosité.