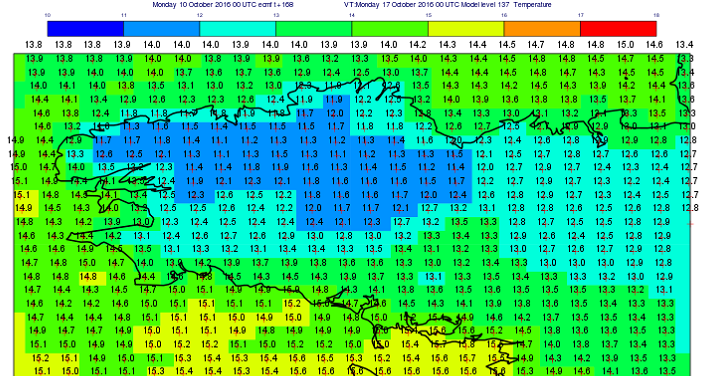
Assimilation des données météorologiques

Les moyens d’observation météorologique (satellites et stations au sol) fournissent une très grande quantité de données météorologiques, qu’il faut traiter pour établir l’état de l’atmosphère au départ du modèle de prévision. C’est ce traitement que l’on appelle l’assimilation des données. Il doit aboutir à une valeur de chacun des paramètres de l’atmosphère dans chaque maille du modèle. Cette étape initiale de la prévision du temps est cruciale car toute erreur initiale a la propriété de se propager et de contaminer progressivement toute l’atmosphère.

1. Le défi du point de départ d’une prévision du temps

Pour prévoir le temps, les grands centres météorologiques utilisent un modèle de prévision qui simule l’évolution de l’atmosphère pour les heures ou les jours à venir. Ce modèle utilise les équations de la mécanique des fluides (lien vers article « Modéliser l’atmosphère : une gageure devenue un succès »), qui sont des équations d’évolution dans le temps : connaissant la solution à un instant donné, on peut obtenir leur solution à tout instant futur. Ces équations sont combinées à d’autres comme celles qui caractérisent les changements d’état de l’eau présente au sein de l’atmosphère ou encore les interactions avec la surface terrestre.

Les prévisions du temps sont donc obtenues en lançant ces modèles de prévision sur une période de temps donnée, mais encore faut-il connaître le point de départ. Pour cela, on s’appuie sur l’assimilation de données, qui permet de passer des données météorologiques, collectées à l’instant du point de départ, aux valeurs des paramètres du modèle au même instant mais pour chacune de ses mailles élémentaires.

2. Les données météorologiques

Le système d’observation de l’atmosphère que nous connaissons aujourd’hui a été développé tout au long des derniers siècles, mais l’invention des radiosondes en 1928 a fourni un premier jeu de données décisif, permettant d’obtenir un moyen de sonder la structure tri-dimensionnelle de l’atmosphère. La deuxième guerre mondiale a accéléré le déploiement d’un réseau global de mesures par radiosonde ajoutées aux mesures au sol. La mise en place de la Veille Météorologique Mondiale en 1963 a aussi permis la fondation d’une structure remarquable, visant à maintenir un réseau de mesures météorologiques à l’échelle du globe et à assurer la disponibilité en temps réel de ces données pour l’ensemble des membres de l’Organisation Météorologique Mondiale (OMM).

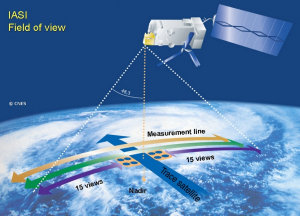
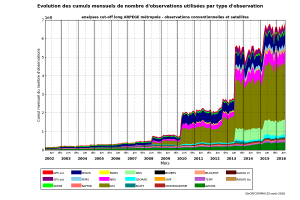
Les données dites aujourd’hui conventionnelles comprennent les observations fournies par les stations au sol, les radiosondages, les capteurs embarqués sur des avions de ligne et les navires de commerce ou installés sur des bouées ancrées ou dérivantes. Mais ces données ne représentent plus aujourd’hui qu’environ 10% du volume total car 90% des données sont désormais fournies par les satellites (Figure 1). La croissance du nombre de données collectées est très rapide (Figure 2) suite à l’augmentation permanente des données fournies par les satellites. Le nombre de données prises en compte à Météo-France pour effectuer les prévisions sur l’ensemble du globe terrestre est maintenant de l’ordre de 20 millions par jour.

3. Bref historique de l’assimilation de données

Dans les premières tentatives de prévision numérique du temps, Richardson en 1922 [1] puis Charney en 1950 [2] reportaient sur une carte les données météorologiques collectées pour un paramètre donné (par exemple la température près du sol) puis traçaient à la main des isolignes de ce paramètre (comme les courbes de niveau sur une carte géographique) et enfin transformaient en valeurs numériques ces isolignes pour chacune des mailles du modèle de prévision. Ce procédé très consommateur en temps est inenvisageable aujourd’hui.

Par la suite, différentes techniques ont été proposées pour automatiser ce processus manuel. Une de ces techniques reposait sur l’idée que la valeur d’un paramètre du modèle pour un point donné peut être évaluée en faisant une moyenne des mesures de ce même paramètre disponibles autour de ce point et en donnant un poids moindre aux mesures les plus éloignées. Bien que fournissant une ébauche de la valeur des paramètres du modèle pour le point de départ de la prévision, ce type de méthode souffrait cependant d’un certain nombre de limitations qui ont été levées par la suite et qui font l’objet des paragraphes suivants.

4. Comment trouver les valeurs les plus vraisemblables des paramètres météorologiques ?

En fait les données des paramètres météorologiques collectées tout autour du globe sont imparfaites. Le plus souvent, elles donnent une indication de la vraie valeur d’un paramètre météorologique en un lieu et un temps donnés, mais avec une plage d’erreur qui dépend de l’instrument qui a fourni cette donnée. On sait par exemple que les mesures fournies par les capteurs de température du réseau terrestre ont une plage d’erreur assez faible, mais qu’au contraire certaines observations fournies par les instruments embarqués sur les satellites peuvent fournir des mesures qui s’éloignent beaucoup plus des valeurs réelles. Ces erreurs ont par ailleurs un caractère aléatoire et sont donc inconnues au moment de la mesure. Ceci veut dire que, même si une donnée est disponible pour une maille du modèle au point de départ de la prévision, cet état initial sera le plus souvent erroné, ce qui limitera la qualité de la prévision du paramètre aux instants suivants.

De manière à remédier à cette incertitude sur les mesures météorologiques, une des idées maîtresses de l’assimilation de données consiste à combiner plusieurs mesures en un point donné, pour obtenir une meilleure estimation de la valeur vraie du paramètre recherché. D’autre part, on va chercher à ce que cette combinaison soit la meilleure possible. La combinaison choisie est une pondération des différentes données disponibles avec des poids directement liés à ce que l’on appelle la précision d’une mesure. Cette précision est simplement définie comme l’inverse de l’amplitude moyenne des carrés des écarts entre la mesure fournie par un instrument et un instrument étalon sans erreur. On parle aussi en termes statistiques de la variance des erreurs de mesure associée à un instrument donné. Un instrument dont la variance des erreurs de mesure est grande aura donc une précision faible et, au contraire, une précision grande si sa variance des erreurs d’observation est faible. Il est donc facile de voir que la combinaison choisie donnera plus de poids aux observations précises qu’aux observations peu précises.

5. Un problème de moindres carrés

Le meilleur estimateur correspond à la solution d’un problème de moindres carrés pondérés. Une telle approche a été a peu près simultanément proposée par Legendre [3] et Gauss [4], il y a un peu plus de deux siècles. Appliquée à notre problème d’estimation, cette méthode revient à chercher les valeurs d’un paramètre pour l’ensemble des mailles du modèle qui soient les plus proches possible des mesures disponibles. Ceci peut être obtenu en minimisant la somme des carrés des écarts entre ces valeurs estimées et les mesures, d’où cette expression moindres carrés. De manière à prendre en compte les amplitudes attendues des différentes mesures, chacun de ces écarts au carré est pondéré par la variance des erreurs de chacune des mesures.

Cette approche n’a cependant de sens que si le nombre et la distribution géographique des mesures disponibles coïncident, au minimum, avec ceux des valeurs que l’on cherche (la valeur d’un ou de plusieurs paramètres pour l’ensemble des mailles du modèle). En pratique ce n’est pas le cas, même avec l’augmentation rapide du nombre de mesures, car il y a simultanément une autre évolution rapide visant à augmenter le nombre de mailles élémentaires, de manière à représenter de manière toujours plus fine les phénomènes météorologiques. On a déjà indiqué qu’aujourd’hui le nombre de mesures disponibles sur une fourchette temporelle de 6 heures est de l’ordre de quelques millions, alors que le nombre de variables pour l’ensemble des mailles d’un modèle de prévision est plutôt de l’ordre du milliard ! Heureusement, cette indétermination majeure peut être levée en mettant en place un algorithme adéquat qui combine les mesures disponibles avec une autre source d’information.

6. Un cycle continu de prévisions / corrections

L’idée de combiner les mesures à une ébauche de la solution fournie par une prévision récente de l’état recherché est similaire à l’algorithme proposé par Kalman [5] et appelé filtre de Kalman. Une première application majeure d’un tel algorithme est apparue dans les années 60 pour des problèmes d’optimisation de trajectoire dans le cadre du programme Apollo.

Cet algorithme s’appuie sur un cycle régulier de prévisions suivies de corrections par les dernières mesures disponibles. Pour les centres de prévision numérique du temps, ce cycle est typiquement répété toutes les 6 heures pour les modèles de prévision sur l’ensemble du globe terrestre (comme le modèle global ARPEGE). Il est généralement plus court pour les modèles à échelle plus fine centrés sur un domaine d’intérêt particulier (1 heure pour le modèle AROME centré sur la France). La phase de correction, ou de mise à jour, consiste à calculer, dans un premier temps, les écarts entre la prévision et l’ensemble des observations disponibles. Ces écarts sont appelés innovations, puisqu’ils fournissent une source d’innovation par rapport à la prévision. La correction à apporter à la prévision s’obtient ensuite comme une pondération des innovations en suivant les mêmes principes que l’estimation linéaire statistique présentée plus haut. Les poids donnés à chacun des écarts entre des mesures et la prévision vont ainsi dépendre de la précision relative de ces mesures, mais aussi, et c’est là la grande nouveauté introduite par le filtre de Kalman, de l’amplitude et de la structure spatiale moyennes des erreurs de la prévision.

Dans la forme la plus complète du filtre de Kalman, telle qu’elle peut être utilisée pour des problèmes de petite taille, l’algorithme donne aussi une manière d’obtenir une estimation en tout lieu de la précision des prévisions qui en découlent. Ceci n’est cependant hélas pas possible pour les problèmes de très grande taille rencontrés en prévision numérique du temps car le nombre de calculs nécessaires devient alors trop élevé. On verra un peu plus loin comment on peut se rapprocher de cette estimation de la précision des prévisions à un coût plus faible.

A partir du moment où l’on combine une prévision et des mesures, il est facile de voir que la question de l’indétermination du problème de moindres carrés soulevée au paragraphe précédent disparaît. En effet, si le nombre de variables du modèle à estimer est de l’ordre du milliard, le fait d’ajouter à la dizaine de millions de mesures les valeurs fournies par une prévision revient à ajouter d’un seul coup ce même milliard de paramètres du modèle. Ainsi, le nombre d’informations disponibles (mesures + paramètres prévus) devient bien supérieur au nombre de valeurs que l’on cherche (paramètres du modèle à un instant). On peut aussi considérer les valeurs fournies par la prévision comme des mesures additionnelles particulières.

7. La notion d’opérateur d’observation

Pour résoudre le problème de l’assimilation de données, des difficultés subsistent lorsque l’on cherche à les appliquer à un domaine comme la météorologie. Une de ces difficultés est en effet liée au fait qu’aujourd’hui un grand nombre des mesures prises en compte ne sont pas de même nature que les variables manipulées par le modèle de prévision. C’est le cas pour la plupart des données fournies par les instruments de mesure embarqués sur les satellites. Le plus souvent un instrument satellite mesure en effet plutôt un rayonnement émis depuis la surface ou un élément de la colonne atmosphérique qu’il surplombe. Pour pouvoir comparer ces mesures aux variables du modèle, il faut donc transformer au préalable les variables du modèle en rayonnement, en appliquant un calcul spécifique, que l’on appelle opérateur d’observation. On sait en effet passer de la colonne de température et d’humidité qui se trouve sous un satellite au rayonnement émis par cette colonne. L’utilisation de ces opérateurs d’observation permet ainsi d’utiliser une gamme très étendue de mesures comme les données satellites mais aussi des données mesurées par des radars terrestres qui sont eux des instruments dits actifs émettant une radiation qui se réfléchit sur la pluie ou la grêle. Le développement de ces opérateurs d’observation a constitué une avancée significative dans l’assimilation de données.

8. Détermination pratique de la solution

Pour résoudre le problème de moindres carrés introduit plus haut, il reste encore à trouver un moyen d’obtenir le jeu de variables atmosphériques qui soit le plus près possible des mesures collectées. Pour prendre en compte une mesure qui ne correspond pas directement à l’une des variables du modèle, on devra donc appliquer au préalable à ce jeu de variables du modèle l’opérateur d’observation correspondant à cette mesure et c’est le résultat de cette opération que l’on comparera à la mesure assimilée. On est donc capable d’écrire la somme des écarts au carré entre les variables du modèle et les mesures, complétée par la somme des écarts aux variables du modèle fournies par la prévision. On se trouve ainsi avec une somme de carrés d’écarts comprenant notamment une dizaine de millions d’écarts aux observations (dans le cas d’un modèle global) et dépendant d’un milliard de variables (toutes les valeurs possibles des variables du modèle pour chacune des mailles élémentaires du modèle).

Le but est de trouver le jeu des variables du modèle qui rend cette somme de carrés la plus petite possible. On cherche ainsi le minimum de cette distance entre les variables du modèle et les mesures (comprenant implicitement la prévision), que l’on appelle aussi souvent fonction-coût, terme que l’on rencontre dans les problèmes d’optimisation, auquel s’apparente effectivement ce problème de moindres carrés. Bien que le problème que l’on traite alors contienne un nombre énorme de possibilités, il apparaît heureusement que le minimum recherché peut être obtenu par un processus itératif, avec un nombre d’itérations qui ne dépasse pas la centaine. Le processus itératif repose sur l’utilisation d’algorithmes de minimisation bien adaptés à ces problèmes de moindres carrés. Une telle approche est aujourd’hui utilisée par l’ensemble des grands centres de prévision numérique. Ce type d’algorithme est aussi appelé 3D-Var, 3D car il s’agit d’un problème tridimensionnel (3 dimensions spatiales, x, y, z) et Var car une telle méthode rentre dans la classe des algorithmes variationnels (où l’on s’intéresse aux variations d’une fonction-coût).

9. Prise en compte de la dimension temporelle

On a vu un peu plus haut que la nature très diverse des mesures collectées aujourd’hui nécessitait de transformer les variables du modèle, en leur appliquant des opérateurs d’observation, pour pouvoir les comparer aux observations. En fait, la diversité des observations est encore compliquée par le fait que beaucoup d’observations sont désormais effectuées de manière quasi-continue dans le temps, ce qui rend difficile la comparaison entre un jeu de variables du modèle à un instant particulier (à partir duquel on veut lancer une prévision sur quelques jours) et les données effectuées autour de cet instant.

Une approche élégante a été proposée et développée dans les années 80-90 pour résoudre cette difficulté.

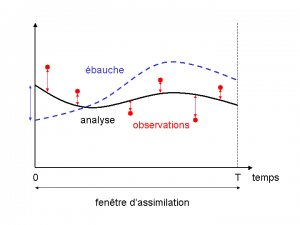
Elle consiste à regrouper les observations sur des intervalles de temps contigus, que l’on appelle fenêtres d’assimilation. Pour un modèle global, ces fenêtres d’assimilation ont le plus souvent une durée de 6 heures et sont centrées sur les heures dites synoptiques (0h, 6h, 12h, 18h), auxquelles sont effectués historiquement les radiosondages de l’atmosphère deux ou quatre fois par jour. On cherche ensuite, au début de chaque fenêtre d’assimilation, le jeu de variables du modèle qui donne le point de départ de la prévision le plus proche des mesures tout au long de la fenêtre d’assimilation (cette prévision est donc faite sur les 6h de la fenêtre d’assimilation). On obtient ainsi un état des variables du modèle qui découle de l’ensemble des données collectées durant une fenêtre d’assimilation donnée et à partir duquel on peut alors effectuer des prévisions sur plusieurs jours.

Ce type d’approche s’apparente toujours à un problème de minimisation de moindres carrés, qui peut encore être résolu par une méthode itérative. On parle d’approche 4D-Var, 4D car il s’agit maintenant d’un problème à quatre dimensions (3 dimensions spatiales, x, y, z et une dimension temporelle t) (Figure 3). La mise en place des algorithmes 4D-Var a permis une meilleure prise en compte des observations se traduisant par une amélioration de la qualité des prévisions.

10. Évolutions attendues de l’assimilation de données

L’utilisation d’un nombre croissant d’observations permet d’améliorer la qualité des prévisions. Cette amélioration découle aussi en grande partie de la progression des techniques d’assimilation de données. Un effort particulier est fait aujourd’hui pour parvenir à une meilleure représentation de l’incertitude à accorder à la prévision utilisée dans le cycle des prévisions / corrections. Pour cela, l’idée est de s’appuyer sur la mise en œuvre d’un ensemble de tels cycles de prévisions / corrections, dans lesquels les deux sources d’information (la prévision et les mesures) sont perturbées. La dispersion des prévisions fournies par un tel ensemble permet alors de chiffrer l’incertitude sur les prévisions et s’apparente ainsi au filtre de Kalman mais avec un coût raisonnable. On parle alors de filtre de Kalman d’ensemble (EnKF). D’autres sujets importants font également l’objet de développements particuliers comme la meilleure description des incertitudes à associer aux mesures. Un des points de focalisation de la communauté assimilation porte par ailleurs sur la recherche d’algorithmes d’assimilation qui se prêteront le mieux à une application sur les futures générations de supercalculateurs qui vont comprendre des millions de processeurs !

 

---

Références et notes

[1] L.F. Richardson, Weather prediction by numerical process, Cambridge University Press, Cambridge, Reprinted by Dover (1965, New York) with a new introduction by Sydney Chapman, 1922.

[2] Charney, J. G., R. Fjortoft, and J. von Neuman, Numerical integration of the barotropic vorticity equation, Tellus 2, 237-254, 1950.

[3] A.M. Legendre, Nouvelles méthodes pour la détermination des orbites des comètes, Paris, Firmin Didot, 1805.

[4] C.F. Gauss, Theoria Motus Corporum Coelestium, Université de Gand, 1809.

[5] R.E. Kalman, A New Approach to Linear Filtering and Prediction Problems, Transaction of the ASME – Journal of Basic Engineering, Vol. 82, p. 35-45, 1960.