The turbulent wake
PDF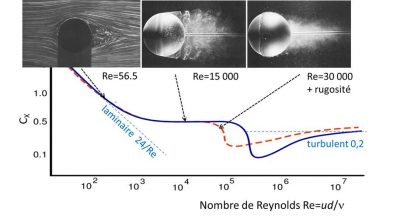
For a moderate value, Re=56.5, we see that the trajectories are detached from the sphere but only on its downstream part, unlike the symmetrical flow obtained at very low Re (see Figure 2 of the article). This detachment still has little effect on the drag coefficient, whose law remains close to that of the laminar regime in 24/Re, as can be seen on the blue curve.
At the larger Re, the flow consists upstream of a thin sheared layer enveloping the surface of the sphere, called the boundary layer, while downstream it is turbulent. The wake, visualized by the injection of smoke, occupies a large cross section, corresponding to a fairly large drag coefficient CX≃0,5, a quasi-constant value when Re is between 103 and 105.
Above Re=105, the drag drops strangely and then stabilizes at a value close to 0.2. This lower Re drop can be reproduced by disturbing the boundary layer with a roughness or an annular wire stuck on the sphere, which is the case of the photo on the right, at Re=30000. We then see that the boundary layer itself becomes turbulent, and this has the effect of delaying its disbonding, leading to a narrower wake. This is the explanation for the drop in the drag coefficient.
It is to produce such a reduction in drag that golf balls are not smooth but honeycombed: for a speed of 50 m/s and a diameter of 4 cm, we have Re=2 105, and we can see on the figure that for this value, the drag for a rough sphere (red dotted line) is indeed lower than that of a smooth sphere.
The case of very large Reynolds numbers can be seen as the borderline case of a very low viscosity. A fluid with strictly zero viscosity would slide frictionlessly over the obstacle, and its flow would represent a kind of ideal where the upstream and downstream would be symmetrical and laminar, and where the drag would cancel each other out. However, this theoretical limit is never reached, which is the paradox of D’Alembert. The explanation lies in the fact that the viscosity, however low it may be, always produces a boundary layer, thicker downstream than upstream, which imposes an asymmetry between upstream and downstream. In addition, at very low viscosity, the boundary layer becomes unstable and feeds wake turbulence, leading to the non-zero drag boundary value observed at very large Reynolds numbers.




