急流
急流是指大气中狭窄的强西风带。为了解释这一现象,我们常将其与花样滑冰运动员的旋转进行类比,二者都符合快速旋转运动的一大特征,即角动量守恒。然而,在大气边界层,气流会受到地面摩擦力作用;此外,大气湍流也会导致能量的耗散。所以,急流的实际风速要明显低于根据角动量守恒公式推算出的理论值。
1.从花样滑冰到急流
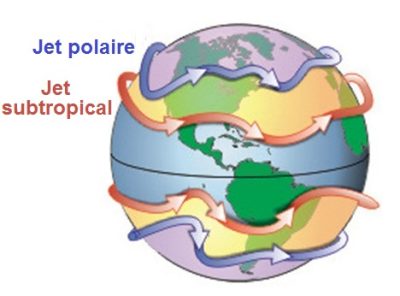
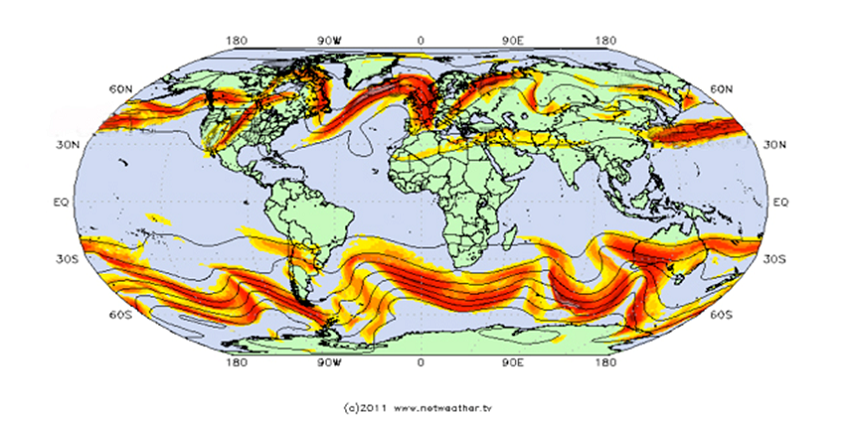
20世纪,得益于航空技术的发展,气象学家得以更多地观测急流,而这也让他们的心中升起一个挥之不去的谜团:为什么这些风的移动方向和地球的自转方向一致,都是自西向东,却还能形成四支环绕地球的强风带呢?诞生于地球旋转的风,其速度却比地球旋转的速度更快,听上去的确自相矛盾。图1是全球急流分布的示意图,这张图曾在《环境百科全书》的另一篇文章中出现过(详见《《大气环流及其构成》),体现了急流位置的瞬时性和不稳定性。为了解开上述谜团,本文将基于旋转系统的重要性质——角动量守恒(conservation of the angular momentum),分别解释极地急流和副热带急流的形成原因。感兴趣的读者可以在经典教材或课程中找到对这一性质的详细说明[1](详见《动力学定律》),在本文中,我们将仅从守恒的角度出发,解释并评估这一性质对急流造成的影响。
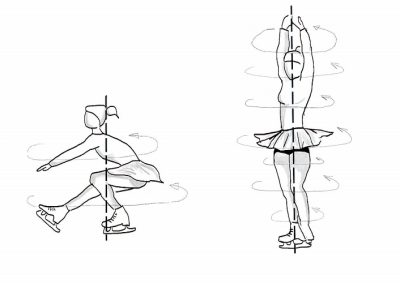
这种守恒性是如何转化的呢?我们可以借助花样滑冰这一广为人知的例子来理解此问题——当滑冰运动员沿身体中轴收紧全身,他们的转速会非常快(图2)。首先,在整个旋转过程的开始阶段,他们一条腿弯曲撑地,同时尽可能伸长另一条腿和两条手臂,来获得尽可能大的平均半径r1(r1 ≈ 0.8 m)。通过动量和平均半径,可获得一定的角速度ω1和初始角动量[2]mω1(r1)2,式中m为常量,表示滑冰者的质量。开始旋转后,如图2所示,他们迅速收紧四肢,使自己的平均半径大幅缩短(r2 ≈ 0.3 m)。为了保持运动员身体的角动量守恒,半径的减少必须通过角速度的增加来补偿,因此可推算出ω2=ω1(r1)2/(r2)2=7ω1。因此,初始转速为每秒2圈的滑冰运动员最终能够达到每秒接近2 × 7 = 14圈的速度,足以让观众眼花缭乱。然而,尽管空气的摩擦力很小,冰鞋在冰上的摩擦力却很大,所以他们很快就会减慢速度,然后停止旋转。
在下文中,我们将会看到,这种守恒性是许多重要大气现象的基础,其中包括本文的主题——急流。同时,在其他行星、恒星乃至星系中观测到的许多现象也可以用角动量守恒来解释,如土星环、集中于太阳纬度70°的太阳风、吸积盘等。
2.副热带急流
让我们假设存在这样一个气团,如文章《信风的关键作用》中所述,其在赤道地区受热,以接近地球自转线速度的绝对线速度(即1600 km/h)离开地面,上升至对流层顶,在该纬度,这一高度接近15 km。绝对线速度Va 指的是地球上的物体相对于太空中不随地球旋转的观察者的运动速度;相对线速度Vr 则与之相反,指的是物体相对于与地球一起旋转的观察者的运动速度。该气团随后进入哈得莱环流(详见《大气环流及其构成》)。在上述旋转系统中,气团在移动路径上必然受到角动量守恒[3]的约束(详见《动力学定律》)。
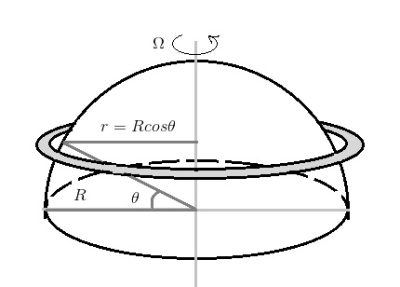
因为质量m为常量,所以气团的角动量守恒(mVar)可以简化为Var的守恒。其中,绝对线速度Va是行星的自转线速度Ωr(Ω为地球自转角速度)和气团的相对线速度Vr之和。因此,该旋转系统中的守恒方程可记为:Var = (Ωr+Vr)r。假定地球为半径为R的球体,在赤道地区的低空,纬度和相对线速度皆为0,该守恒量Var等于ΩR2。而赤道地区的对流层顶距地面仅约15 km,远远小于地球半径(R ≈ 6400km),因此可以近似认为,此处与地轴的距离仍然等于地球半径。由此可知,对流层顶的Var与低空相同,都近似等于ΩR2。
而在哈得莱环流的上部,随着气流向极地方向移动,纬度θ由0°逐渐增加到接近±30°,到地轴的距离变为r=Rcosθ(图3)。根据角动量守恒可推导出(ΩRcosθ+Vr )Rcosθ =ΩR2,即Vr = ΩR(1-cos2θ)/cosθ。在赤道,纬度θ = 0°,气流的相对线速度为零,这意味着空气与地球的旋转速度相同。而到了纬度θ = 30°处,即副热带急流所在地区,角动量守恒导致相对线速度变为Vr ≈ 0.29 ΩR ≈ 460 km/h,这意味着空气的旋转比地球自转更快。然而,事实上,纬度θ = 30°地区的风速通常不到100 km/h,远小于460这一理论值。这是因为就像滑冰运动员的制动一样,摩擦和湍流会导致动量损失,致使风速由预测值降低到实测值。
3.强劲的极地急流
相比于副热带急流,极地急流更具代表性,风速也更快,可达300 km/h左右。其位于费雷尔环流和极地环流的交界处(详见《大气环流及其构成》),平均纬度接近θ=±70°。如果我们将相应的cosθ = 1/2代入前文所述的关系式,可得到相对线速度Vr ≃ 2400 km/h。当然,这一估算并不完全合理,因为到达该纬度对流层顶的气团与赤道地区的气团实际上并非同一个。但是,从中足以看出,随着对流层顶与地轴之间距离的减小,当纬度足够大时,相对线速度可能会变得非常大。
到达纬度θ=±70°处对流层顶的气团有两大来源:费雷尔环流或极地地区。其中,来自费雷尔环流的气团会经过近地面的大气边界层,受到较大的摩擦。如果气团的角速度Ω保持不变,那么其离开地面时,角动量将接近3ΩR2/4。如果上升至对流层顶的过程中没有明显的能量耗散,根据前文所述的公式,可推算出相对线速度为Vr ≈ 1600 km/h。与副热带急流类似,计入摩擦损耗后,实际风速会大大降低,约为300 km/h。而来自极地地区的气团由于与地轴相距过近,角动量很小,因此对急流风速的贡献也较小,更多的是影响急流位置。在近地面,极地环流中向南移动的气流与费雷尔环流向北移动的气流交汇,将辐合区锁定在纬度θ=±70°附近。
4.大幅变缓的气流
令人好奇的是,为什么急流的实际风速远远小于由角动量守恒定律推算出的理论值呢?为什么会存在如此巨大的能量损耗,以至于每条急流实际的风速只有理论值的1/5左右?对副热带急流而言,其位于哈得莱环流的上部,也就是离地面约15 km的高空中。这一高度远超大气边界层的厚度(约几百米),几乎不存在粘性摩擦造成的耗损。那么,真正导致副热带急流能量损耗、风速变小的原因是什么呢?答案其实很简单。在副热带急流气团的发源地赤道地区,存在高度不稳定且复杂多变的对流活动。这些对流活动发端于大陆上空暖空气和海洋上空冷空气的交界处。受白天太阳辐射影响,较轻的暖空气上升,较重的冷空气下沉,二者共同作用,催生并维持了一个具有强对流活动的环流——即赤道辐合带(ITCZ)。在ITCZ中,湍流活动旺盛,并且经常发生暴风雨。这些强烈的湍流扰动从主要气流处吸收了大量的动能,并借助粘性力,使之以热能形式耗散。通过此类过程,上升的气流失去了部分初始角动量。这也是“赤道无风带”(doldrums)的结果。(详见《信风的关键作用》)。
那么,又是什么造成了极地急流风速的减缓呢?在花样滑冰的例子中,由于冰面的摩擦,滑冰运动员只能高速旋转几圈,在几秒内就会急剧减速。同理,摩擦对极地急流也有着相同的作用。极地急流的气团来源于费雷尔环流或极地环流。气团在经过近地面的大气边界层时,局地的湍流作用使得粘性摩擦增大。因此,当费雷尔环流和极地环流交汇时,上升气团的部分初始角动量就已经在摩擦力的作用下耗散了。
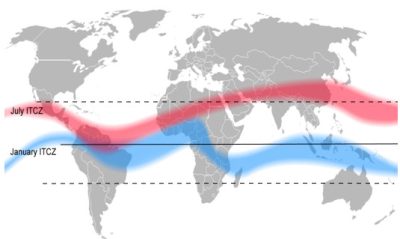
正如我们在图1中所看到的,急流本身并不是规则且稳定的风,和对流层一样,它也受到周期性变化造成的不稳定性的影响。首先,如图4所示,季节更替导致赤道辐合带(ITCZ)在夏季向北移动,在冬季向南移动(详见《信风的关键作用》)。其次,大陆上空的空气相对干燥,而海洋上空的空气则水汽充沛,两者湿度的差异导致了密度的不同,一旦交汇即会引发不稳定。最后,夜间空气冷却,大气层结较为稳定。而到了白天,受到辐射加热的作用,地表升温导致近地面暖空气上升。由于上层的空气偏冷,下层的空气较暖,两者温度的差异也会导致密度的不同,进而激发强烈的对流。这三种机制各不相同,唯一的共同点是都有利于不稳定和湍流的发生,将急流的平均风速拉低至角动量守恒下理论值的五分之一。
滑冰和急流的例子,揭示了角动量守恒在快速旋转的力学系统中的显著影响。虽然与地面和空气的摩擦,以及湍流混合都会消耗角动量,但这种守恒性仍然是许多重要大气现象的基础。在管理洲际商业航班时应该考虑到这一点。为了减少燃料消耗,从欧洲飞往美国的航班应从北边绕过极地急流,而回程航班则应借急流之力。
参考资料及说明
封面照片:www.netweather.tv, 2011
[1] https://fr.wikipedia.org/wiki/Moment_kinetics_(classical_mechanics)
[2] 角动量是物体质量、其绝对(或伽利略)参照系中的角速度和其平均旋转半径平方三者的乘积。
[3] https://fr.wikipedia.org/wiki/Moment_kinetics_(classical_mechanics)
环境百科全书由环境和能源百科全书协会出版 (www.a3e.fr),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: MOREAU René, FLOR Jan-Bert (2024年3月11日), 急流, 环境百科全书,咨询于 2024年4月20日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/air-zh/jet-streams/.
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。









