动力学定律

牛顿定律将加速度和力关联起来,它是现代物理学的发端。牛顿定律可应用于天气图,它是天气和气候预报模型的核心。自古以来,人们就用对力的直观概念来理解静态平衡。我们可以据此设计建筑物的拱顶,使用杠杆,或者描述阿基米德浮力作用下处于平衡状态的流体。伽利略发现的惯性原理为提出牛顿运动定律奠定了基础。牛顿运动定律的重要意义是成功解释了行星、卫星以及潮汐的运动现象。由于需要大量的数学专门知识,牛顿定律在解释大气或海洋等复杂系统的运动时遇到困难。直到计算机问世后,我们才能求解其动力学方程。不过,具有全局约束的动量、能量、动量矩守恒定律使我们能比较直观地理解某些现象。
1、力的平衡
力代表着物体受到的某种机械作用,它具有明确的物理来源,如万有引力(重力)、带电粒子上的电力、电缆受到的接触力或拉力,又比如弹簧的弹力。与物理学的许多基本概念一样,力本身很难定义,但可以通过实验案例以及力与其他物理量的数学关系来研究。
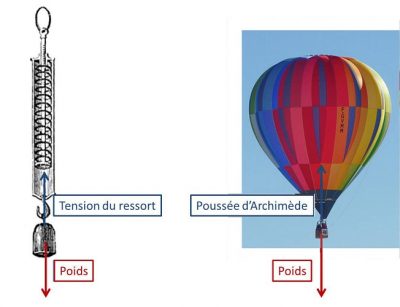
[图片来源:《基础物理学专著》,德里恩(Drion)和弗奈特(Fernet),1885]
(图1a:Tension du ressort 弹簧的拉力,Poids 重力;图1b:Poussée d’Archiméde阿基米德浮力,Poids 重力)
力的大小(或模量)、方向和作用点是力的三要素,力在数学上可用矢量来表示。作用在静止物体上的合力一定为零。通过测量弹簧相对于静止状态的伸长量可以得到力的大小(图1)。通过连续添加相同质量砝码的实验,可证实弹簧的伸长量与其所受力的大小成正比。这样,校准后的弹簧测力计就可以用来测量力的大小了。热气球在空气中悬浮不动时,总重量与阿基米德浮力相平衡,阿基米德浮力与热气球所排开空气的质量大小相等,方向相反。这正是气囊周围的大气压力作用的结果:由于大气压力随高度升高而降低,气囊底部的压力高于顶部,从而变为一个向上的净压力。实际上,压力和重力之间的这种平衡适用于任意体积的流体,即所谓的流体静力平衡(参见《压强、温度和热量》)。正是由于这种平衡,大气层中的空气和水才不会因受重力而落到地上。空气受热后,密度降低,单位体积的质量就会降低,而受周围空气的重量控制,压力又保持不变,这样一来,平衡状态就会被打破,导致热气球加速垂直上升。同理,在大气层中,局部气团受太阳辐射加热后也会趋于上升,这就是对流的原理。

[图片来源:http://olive-art.weebly.com/uploads/2/6/0/5/26053332/6555663_orig.jpg]
一般来说,力的平衡必须用矢量表示,这是计算建筑结构中的力的基础(见图2)。每个质点(例如纱线的交点),处于平衡状态时,力的矢量和必须为零,如图3a所示。因此,已知力F3以及角θ1和θ2,F1和F2的大小可以通过几何结构或沿垂直轴和水平轴作矢量投影来计算。在物理学中,一个实际物体(如固体)被描述为一组由内力保持在一起的质点系。这些内力应与外力(如重力或与其他物体的接触力)区分开。内力由于作用和反作用原理而相互抵消,因此物体的平衡需要抵消掉外力。
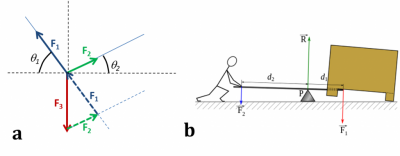
然而,实际物体的平衡不仅要抵消掉外力,还要抵消掉总力矩,以免产生旋转。力矩的定义是垂直于轴线投影的力与转动中心点到力的作用线的距离的乘积。图3b所示的杠杆是一个经典的例子。在平衡状态下,或是慢速运动的准平衡状态下,力矩相抵消的要求是F1d1=F2d2(这里的力是垂直于轴线的),这样就可以通过减小到转动中心点的距离来增加所施加的力(通常,F1表示力的强度,而1表示矢量)。在这里通常只考虑与杠杆轴有关的力矩,因此地面反作用力力矩会自行抵消。如果是对于任一数轴,则还需要在此基础上考虑地面的反作用力,这样计算才能得到相同的结果。
2、力和加速度
离开静力学领域,我们来看加速度。根据著名的牛顿运动定律F=mg,物体的加速度与作用在物体上的合力F有关,m是物体的质量,g是加速度矢量。由此可以将力的单位牛顿(N)定义为使质量为1kg的物体产生1 m/s2加速度的力,即1N=1kg·m/s2。
一个不受任何外力的物体将保持静止或匀速直线运动,这就是由伽利略(1564-1642)首先提出的惯性原理。这个原理在当时并不是很直观,因为在日常生活中,任何运动在不受力的情况下都会趋于停止。现在,这种减速(负加速度)归因于与速度方向相反的摩擦力。但在星际空间,摩擦力可以忽略不计。牛顿(1643-1727)的巨大成功在于他通过一个简单的定律从数学上描述了行星和卫星的运动,即万有引力的大小与它们之间的距离r的平方成反比。
牛顿定律的应用需要用到一个数学概念,即导数,它规定了速度和加速度的概念。我们注意到速度v=dz/dt,其中dz是时间间隔dt内的一小段位移。实际上,我们考虑的是个极短时间间隔的极限。同样,加速度记为g=dv/dt。对于恒定的加速度g,速度则与时间成正比,v=gt,很容易证明下降的距离(初始高度z0与高度z之差)z0-z=(1/2)gt2。因此,在重力(g=9.8m/s2)的作用下,地球上的物体要在1s内达到9.8 m/s(35 km/h)的速度,下降高度应为4.9m。
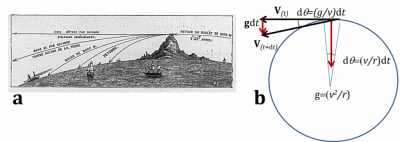
现在牛顿定律普遍用矢量形式表达:即物体可以像前面所说的那样垂直下落,同时因惯性保持其水平速度分量不变。当水平速度足够大时,则必须考虑地球的曲率,如卫星的圆周运动(见图4)。在这个例子中,速度的大小不变,但速度矢量会以与卫星相同的角速度旋转[1]。因而,加速度与速度垂直,并指向地球中心,其值为g=v2/r,如图4所示。因此,对于一颗靠近地球的卫星[2],g=9.8 m/s2,r=6500 km,可得:速度v=(gr)1/2=8 km/s,公转时间(长度40000km)T=5000s (1h 23min)。
这样就能计算出了卫星在地球表面附近运动的速度v=8000m/s(r=6500km,g=9.81m/s2)。如果重力加速度g与1/r2成正比,则圆周运动的速度v=(gr)1/2与1/r1/2成正比,公转周期2πr/v则与r3/2成正比。因此,月球距离地球384000km的月球,即r=384000km,相当于地球半径的60倍,它的公转时间一定是地球附近的卫星的465倍,即27天。这与观测结果是一致的[3]。行星绕太阳公转的周期与r3/2成正比的规律最早是由开普勒(1571-1630)发现的。牛顿通过精准测量行星位置证实了开普勒建立的三大定律。此外,牛顿还解释了圆形轨道是特殊情况,在实际星空中一般行星和卫星的运动轨道为椭圆形,超出排气速度的运动轨道为双曲线。
由于重力本身与质量成正比,因此加速度与质量无关,也就是说所有物体在同一地点都将以相同的加速度坠落。伽利略指出了引力质量和惯性质量之间的这种等效性,并通过著名的比萨斜塔抛落物体的实验(也可能只是想象)来证明。科学家们在没有空气摩擦的真空中又重复了这个实验,结果与伽利略所说的十分吻合。为了向公众展示,阿波罗十五号的宇航员在月球上拍摄了一段影片,比较锤子和羽毛的下落速度[4]。地球上,科学家也在一个巨大的真空室中拍摄了类似的影片[5]。正是由于这个等效原理,卫星上每个失重漂浮起来的物体,都会沿着完全相同的轨道绕地球转动。为了检验新的引力理论所预测的等效原理的偏差,科学家展开了超精密测量。目前,等效原理的相对精度已得到10-13(即十万亿分之一)量级的验证,近期发射的“显微镜”卫星的检验精度将达到10-15。
3、动能和势能
由上述自由落体的例子可得mg(z0-z)=m(1/2)g2t2=(1/2)mv2。这就是由动能(1/2)mv2和势能mgz组成的机械能守恒定律。当物体下落时,动能不断增加的同时,势能也在不断减小,所以总机械能不变(没有摩擦力的情况下)。机械能守恒更加适用于卫星。一般来讲,(1/2)mv2这个速度大小的函数就是动能表达式,但重力势能的表达式需要修改,因为势能受重力会减小。势能只取决于物体的位置,因此物体绕地转一圈后势能会回到相同的值,动能也会回到相同的值,这才符合行星可以无限地持续运动这一基本事实。重力势的定义是用重力势能除以物体的质量。这个势的特征是引力场与围绕它运行的物体本身无关(只要该物体足够小,且没有通过反作用力使行星产生运动)。
机械能的守恒需要一种特殊形式的动力学定律。与重力不同,摩擦力会减少机械能。因此,卫星最终会与残余大气层接触。不过,损失的机械能会转化为热量,因此总能量仍然保持不变(见《什么是能量》)。本质上,热量对应的是气体分子的无序动能。一个均匀的球形星体的势能以变化,所以等势面是一个个同心球面。但是,由于地球的自转和不均匀性,这些同心球面会发生轻微的畸变。平衡状态的海洋表面就是这种等势面(见《海洋环境》)。等势面上运动的物体都保持着相同的势能,由于总能量是守恒的,所以在重力的作用下,它不能单独获得(或失去)速度。反之,如果海洋表面的形状偏离了等势面,表层的水就会流向势能较低的区域,直到将其填满,达到等势面的平衡状态。由于地幔的侵蚀和可塑性,地球的固体表面也在接近等势面。
4、动量
一个质点的动量被定义为质量和速度的乘积。这一定义可以拓展到任何物理系统,只需将每个质点的动量(矢量)相加。很容易证明系统的总动量等于系统的质心(受其总质量影响的惯性中心)的总动量。牛顿运动定律则表明,动量对时间的导数与作用于系统的合力相等。
根据物理学的基本原理,孤立系统的动量是守恒的。换句话说,它的质心作匀速平移运动时,只有外力才能改变这个速度。另一种等效的说法是作用力与反作用力原理,它规定任意一个物体A对任意一个物体B施加力时,都会受到物体B施加的一个大小相等但方向相反的力,而且动力学定律表明,这些内力不会改变整个系统A+B的动量。这就涵盖了上文所讨论的静态平衡条件。
假设知道了初始质量m1和m2以及各质量的初始速度u1和u2,就可以计算出碰撞前的动量m1u1+m2u2,根据动量守恒,就可以确定碰撞后的最终速度。如果进一步假设碰撞是弹性的,即动能m1u12+m2u22守恒,则可以计算出两者的最终速度。如果m1=m2,就可以实现速度的交换(图5a)。再假设碰撞完全没有弹性,即碰撞后相粘的情况下,质量在碰撞后仍是定值,根据动量守恒,可以得到最终速度等于初始速度(m1u1+m2u2)/(m1+m2)的加权平均值。将这些碰撞特性应用到气体分子上,就可以解释粘度现象,即在保持总动量守恒的前提下,流体内部的快速和慢速区域的动量相等。
另一个经典例子是火箭或飞机的推进:无论涉及到何种复杂的机制,推进飞行器的动量与喷射气体的动量始终是大小相等方向相反的。这也适用于万有引力,月球吸引地球的力与地球作用在月球上的引力大小相等,方向相反。因此,地球绕地月系统的惯性中心旋转,这与链球运动员必须身体旋转以补偿链球的反作用力的情况相同(见《潮汐》)。正是这个惯性中心也说明了是地球是沿椭圆轨道绕着太阳旋转而不是太阳绕着地球旋转的。



5、角动量
对于一个质点来说,轴的角动量被定义为到轴的距离与垂直于轴的动量的乘积。这个定义可以推广到实际物体上,例如将一个固体想作是由很多质点组成的,固体的角动量可视作这些质点角动量之和。我们在动力学定律中证明了,动量矩对时间的导数等于作用在系统上的力的合力矩。静力学定律要求作用在系统上的力的合力矩为零。
动量守恒定律规定,内力的力矩会相互抵消,只有外力的力矩才能改变角动量。因此对于固体来说,内聚力不影响动量矩的平衡,正如它不影响动量一样。这是物理学的基本原理,不同于作用力与反作用力原理,但是互为补充。
换句话说,如果没有外力的作用,一个系统不可能自发旋转,也不可能停止最初的旋转。但是,在收缩或伸展时,它的旋转速度可能会发生变化。事实上,对于一个质点来说,力矩一定时,速度u与到轴的距离r的乘积不变,所以速度u与距离r成反比,其角速度与距离的平方成反比。
滑冰运动员以及自然环境中龙卷风和气旋的形成(见《龙卷风:强大的毁灭性漩涡》)都是很典型的例子。地球的自转也是由于形成地球的物质在堆积过程中角速度不断增大形成的。最壮观的例子就是脉冲星(密度极高的恒星)的形成,其旋转周期仅为几秒甚至几毫秒。这些天体往往都是一颗大型恒星坍塌形成的,坍塌发生后,恒星的半径从100万公里收缩到10公里,这种程度的收缩导致该恒星旋转的角速度不断增加,可达100亿倍,从而形成脉冲星(部分角动量随爆炸喷出的气体一起激增)。
实际上,角动量是一个与旋转轴平行的矢量[6],因此它的方向和大小都是不变的。这就是陀螺仪的原理。同样,由于这个性质,地球的自转轴总是与其它星体一致,北极永远指向北极星附近。
[来源:http://hyperphysics.phyastr.gsu.edu/hbase/mechanics/imgmechs/imgmech/topp.gif ]
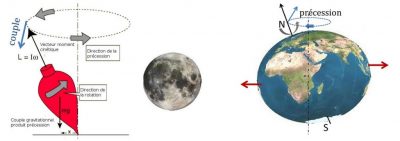
上述性质只在孤立系统中,更准确地说,是在不受外力或没有外力矩的情况下成立。正如垂直于速度的加速度会使速度旋转且大小不变一样,垂直于旋转轴的转矩会使旋转轴产生绕轴的旋转,而角速度保持不改变:这就是在观察陀螺时看到的进动现象,见图6。由于地球极点处的形状是扁平的,地球也会出现类似的效应:月球对地球靠近月球的部分比远离月球的部分有更强的引力,从而产生了一个转矩,又由于地球在自转,因此地轴在以26000年周期缓慢进动(见图6)。极点的方向也以数百年的周期在天球上缓慢移动。这就导致当地球自转轴方向与太阳方向垂直时,地球春秋分点位置的轨道会发生位移,这是我们称这种现象为“岁差”的原因。它也是太阳辐射发生相应变化从而导致间冰期/冰川期交体的原因。
参考资料与说明
封面图片:维基共享http://creativecommons.4rg/licenses/by-sa/2.0 (Uploaded to Flickr as jfpds regular)[CC BY-SA 2.0]。
[1] 角速度Ω是单位时间内所经过的角度,一般用弧度/s表示,所以Ω=v/r 。弧度定义为截取等于半径的圆弧的角度,所以完整的一圈(周长2πr)代表2π弧度,旋转周期为T=2π/Ω=2πr/v。
[2] 为了避免大气摩擦,高度必须达到几百公里,但重力加速度仍然接近地球表面的加速度,轨道半径也与地球相差无几。
[3] 指恒星周期,即行星绕恒星公转一周的所需要的时间。会合周期则是行星环绕恒星公转一周回到从地球的角度观察到的原来的位置所需要的时间,地球上两次观测到满月之间的时间为29.5天。
[4] Apollo 15 Hammer and Feather Drop- Youtube(阿波罗15号的锤子和羽毛坠落)
[5] Brian Cox visits the world’s biggest vacuum chamber – Human Universe: Episode 4 Preview – BBC Two(布莱恩·考克斯参观了世界上最大的真空室—人类宇宙:第四集预览-BBC第二集)
[6] 角动量相对于原点O的定义更为精确,对于点M处的质点m,它是位置矢量OM与动量mu的矢量积,对于一个轴对称的固体,如陀螺或地球,动量矩与旋转轴一致,其值与角速度和惯性矩成正比。
环境百科全书由环境和能源百科全书协会出版 (www.a3e.fr),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: SOMMERIA Joël (2024年4月12日), 动力学定律, 环境百科全书,咨询于 2024年4月25日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/physique-zh/laws-of-dynamics/.
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。