Les jet streams
PDF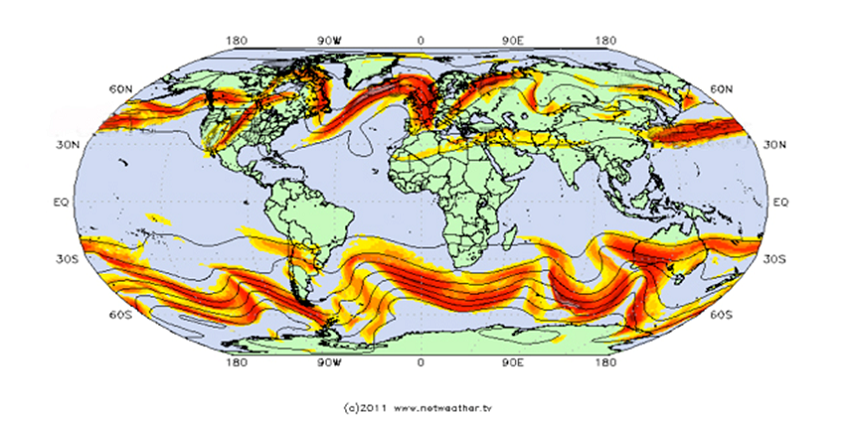
Les jet streams, vents majeurs qui circulent d’ouest en est dans l’atmosphère, peuvent être expliqués par analogie avec la rotation des patineurs sur glace. En effet, ces deux phénomènes possèdent en commun une propriété remarquable des mouvements en rotation rapide : l’invariance du moment cinétique. Néanmoins, en raison du frottement sur le sol dans la couche limite atmosphérique et des prélèvements d’énergie dus à la turbulence, les vitesses de ces vents sont nettement inférieures aux valeurs déduites de cette propriété d’invariance.
1. Du patinage artistique aux jet streams


Comment se traduit cette propriété d’invariance ? L’exemple bien connu pour l’interpréter et la comprendre est la mise en rotation très rapide des patineurs sur glace lorsqu’ils resserrent tout leur corps autour de leur axe vertical (figure 2). Tout d’abord, pour commencer à tourner, ils prennent un appui fort sur l’une de leurs jambes très fléchie, tout en écartant au maximum l’autre jambe et leurs bras. Ils utilisent leur élan et leur rayon moyen r1 rendu aussi grand que possible (r1 ≈ 0,8 m) pour acquérir une certaine vitesse angulaire ω1 et un moment cinétique [2] initial mω1r12, où m désigne la masse du patineur qui va demeurer invariante. Cela fait, ils resserrent rapidement les membres écartés, comme esquissé sur la figure 2, ramenant leur rayon moyen à une valeur r2 bien plus petite que r1, disons r2 ≃ 0,3 m. Pour conserver le moment cinétique du patineur, cette diminution du rayon doit être compensée par une augmentation de la vitesse angulaire, qui devient ω2 ≃ ω1r12/r22 ≃ 7ω1. Ainsi, le patineur capable de se lancer initialement à 2 tours par seconde parvient à tourner à une vitesse voisine de 2 x 7 = 14 tours par seconde, suffisante pour que les spectateurs aient de lui une image floue. Toutefois, si le frottement de l’air est faible, celui du patin sur la glace est important et parvient rapidement à ralentir puis à stopper la rotation du patineur.
Comme nous allons le voir, cette propriété d’invariance est à l’origine de phénomènes atmosphériques importants, dont les jet streams, objet de cet article. De nombreux autres phénomènes visibles sur les planètes (l’anneau de Saturne), dans les étoiles (concentration du vent solaire vers des latitudes solaires de 70°) et dans les galaxies (les disques d’accrétion) peuvent aussi s’interpréter à l’aide de cette propriété d’invariance.
2. Le jet stream subtropical

Isolons par la pensée un paquet d’air soumis à l’ascendance de la région équatoriale commentée dans l’article Le rôle clé des alizés. Il quitte le sol avec une vitesse absolue horizontale proche de celle de la Terre, soit 1600 km/h, et s’élève vers l’altitude limite de la troposphère, proche de 15 km à cette latitude. Par vitesse absolue Va on désigne la vitesse que verrait un observateur très éloigné dans l’espace et qui ne tournerait pas avec la Terre ; au contraire, on appelle vitesse relative Vr celle que voit un observateur solidaire de la Terre. Le paquet d’air s’engage alors dans l’une des cellules de Hadley (Lire La circulation atmosphérique : son organisation). Dans ce système en rotation, son parcours est nécessairement marqué par la conservation de son moment cinétique [3] (Lire Les lois de la dynamique).
L’invariance du moment cinétique de ce paquet d’air se ramène à celle du produit Var puisque la masse m doit aussi être invariante. Or la vitesse absolue Va est la somme de la vitesse d’entraînement de la planète, que l’on peut écrire Ωr en désignant par Ω la vitesse angulaire de la Terre, et de la vitesse relative Vr du paquet d’air par rapport à la Terre. La quantité invariante dans ce système en rotation est donc : Va r = (Ωr+Vr)r. Au voisinage de l’équateur et à basse altitude (latitude nulle et vitesse relative nulle), elle vaut ΩR2 en désignant par R le rayon de la Terre que l’on suppose sphérique. Au sommet de la troposphère, à une altitude proche de 15 km, soit encore à une distance de l’axe voisine de R ≈ 6400km, on peut admettre qu’elle possède la même valeur ΩR2 qu’au niveau du sol.
Dans la partie haute de la cellule de Hadley, en suivant le courant dans le plan méridional, la latitude θ augmente jusque vers des valeurs proches de ±30° et on comprend que la distance à l’axe devient r=Rcosθ (voir Figure 3). La conservation du moment cinétique conduit alors à la relation (ΩR cosθ+Vr)R cosθ = ΩR2 , soit Vr = ΩR(1/cosθ –cosθ). A la latitude de l’équateur (θ=0), elle conduit à une vitesse relative nulle, ce qui signifie que l’air tourne à la même vitesse que la planète solide. Mais, à la latitude θ=30°, typique du jet stream tropical, cette relation conduit à Vr ≃ 0,29 ΩR≃ 460 km/h, ce qui signifie que l’air doit alors tourner plus vite que la planète solide. Cette valeur est très supérieure à la vitesse réelle de ce vent, toujours inférieure à 100 km/h ; mais il est tout à fait compréhensible que les pertes de moment cinétique dues au frottement et à la turbulence soient suffisantes pour ramener cette prédiction à une valeur réaliste. Ces pertes sont l’équivalent atmosphérique du freinage des patineurs sur glace.
3. Le puissant jet stream polaire
C’est de loin le plus rapide des deux puisqu’il atteint des vitesses voisines de 300 km/h ; c’est d’ailleurs celui dont il est question lorsque l’on parle du jet stream au singulier. Sa latitude moyenne, à l’intersection de la cellule de Ferrel et de la cellule polaire (Lire La circulation atmosphérique : son organisation), est proche de ±70°. Si l’on appliquait la relation vue plus haut avec cos θ = 1/2, on trouverait une vitesse relative Vr ≃ 2400 km/h. Cette estimation n’est pas du tout justifiée, car les paquets d’air qui atteignent le haut de la troposphère à cette latitude ne proviennent pas du voisinage de l’équateur. Néanmoins, elle illustre l’énorme potentiel d’accroissement de la vitesse relative lié à la réduction de la distance à l’axe de la Terre quand la latitude devient assez grande.
On a compris que les paquets d’air qui arrivent en haut de la troposphère à des latitudes proche de ±70° proviennent, soit de la cellule de Ferrel, soit des régions polaires. Les premiers ont transité près du sol, dans la couche limite atmosphérique où le frottement est important. S’ils avaient conservé la vitesse angulaire de la planète Ω, leur moment cinétique serait voisin de 3ΩR2/4 lorsqu’ils quittent le sol. S’ils parvenaient en haut de la troposphère sans avoir subi une dissipation d’énergie importante, la même formule conduirait à une vitesse relative Vr ≃ 1600 km/h. Comme pour le jet stream tropical, il est donc nécessaire de prendre en compte le frottement pour aboutir à un ordre de grandeur réaliste, voisin de 300 km/h. Quant à l’air amené par la cellule polaire, puisqu’il vient du voisinage des pôles, où la distance à l’axe est très faible, il n’apporte pas autant de moment cinétique que l’air venu de la cellule de Ferrel. Son influence consiste principalement à localiser la zone de convergence polaire vers une latitude proche de ±70°, entre la cellule de Ferrel où l’air circule vers le nord au voisinage du sol et la cellule polaire où il circule vers le sud.
4. Des courants fortement freinés
On peut se demander pourquoi ces courants demeurent tellement plus lents que les prédictions déduites de la conservation du moment cinétique et pourquoi ils subissent des pertes d’énergie aussi importantes, au point de diviser par 5 environ la vitesse de chacun des jet streams. Dans le cas du jet subtropical, ces pertes ne peuvent pas venir directement du frottement visqueux qui est tout à fait négligeable dans la partie haute de la cellule de Hadley. Celle-ci se trouve en effet à une altitude voisine de 15 km, très supérieure à l’épaisseur de la couche limite atmosphérique, de l’ordre de quelques centaines de mètres. La réponse est assez simple : ces pertes proviennent de l’agitation turbulente intense qui règne dans le courant ascendant de la zone de convergence intertropicale (Inter Tropical Convergence Zone, ou ICTZ), perturbé par les mouvements convectifs très instables et très variables des régions tropicales. Ceux-ci prennent naissance aux interfaces entre l’air chaud situé le jour au-dessus des continents et l’air froid situé au-dessus des océans. Les courants d’air chaud, très léger, s’élèvent ; les courants froids, plus lourds, descendent ; ensemble ils créent et entretiennent de larges cellules animées d’un fort mouvement de convection, très turbulentes et souvent orageuses. C’est cette turbulence qui prélève une part importante de l’énergie cinétique du mouvement principal et la dissipe en chaleur par viscosité, freinant ainsi le courant ascendant qui perd une partie de son moment cinétique initial. On trouve là une conséquence du « pot au noir » des régions tropicales (Lire Le rôle clé des alizés).
Dans l’exemple du patineur, le frottement sur la glace atténue sa rotation en quelques secondes, ce qui permet aux spectateurs d’en voir l’atténuation après plusieurs tours à grande vitesse. Le mécanisme qui freine le jet polaire, alimenté par de l’air qui circule au voisinage du sol dans la cellule de Ferrel ou dans la cellule polaire, est analogue. C’est le frottement visqueux, amplifié par la turbulence locale dans la couche limite atmosphérique présente au voisinage du sol, qui réduit le moment cinétique initial des paquets d’air en ascension vers le haut de la troposphère, à la latitude où la cellule de Ferrel et la cellule polaire convergent.
Comme le suggère la figure 1, les jet streams eux-mêmes sont loin d’être des vents réguliers et stationnaires. Ils sont en effet l’objet d’instabilités excitées par les pulsations périodiques auxquelles la troposphère est soumise. Et la figure 4 montre que les variations saisonnières déplacent la zone de convergence intertropicale (ITCZ, Inter Tropical Convergence Zone) vers le nord en été et vers le sud en hiver (Lire Le rôle clé des alizés). Les alternances entre les continents au-dessus desquels l’air est relativement sec et les océans au-dessus desquels il est au contraire chargé d’humidité contribuent aussi à cette excitation. Enfin, de jour, l’air qui s’élève du voisinage du sol est plus chaud donc plus léger que l’air qui s’est refroidi, alourdi et stabilisé pendant la nuit. Ces différences de température et d’humidité provoquent des variations de masse volumique, qui engendrent des formations convectives très turbulentes. Chacun de ces trois mécanismes possède ses propres caractéristiques, mais ensemble ils nourrissent les instabilités et la turbulence des jet streams, ce qui contribue à réduire leur vitesse moyenne à des valeurs à peu près par 5 fois plus faibles que les prédictions tirées de l’invariance du moment cinétique.

Références et notes
Photo de couverture: www.netweather.tv, 2011
[1] https://fr.wikipedia.org/wiki/Moment_cinétique_(mécanique_classique)
[2] Le moment cinétique est le produit de la masse du corps par sa vitesse angulaire dans le référentiel absolu (ou galiléen) et par le carré de son rayon moyen.
[3] https://fr.wikipedia.org/wiki/Moment_cinétique_(mécanique_classique)
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : MOREAU René, FLOR Jan-Bert (19 septembre 2018), Les jet streams, Encyclopédie de l’Environnement. Consulté le 20 septembre 2024 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/air/les-jet-streams/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.







