The laws of dynamics

Newton’s law linking force and acceleration is at the origin of modern physics. Applied to each plot of fluid, it is at the heart of weather and climate prediction models. The intuitive notion of force has been used since antiquity to understand static equilibria. It allows to design the vaults in architecture, to use a lever, to describe the fluid balance under the effect of Archimedes’ thrust. It was the principle of inertia discovered by Galileo that paved the way for the laws of Newtonian dynamics, whose great success was in explaining the movement of planets and satellites, as well as the tides. This has required a great deal of mathematical expertise, which has its limits for more complex systems such as the atmosphere or the ocean. The resolution of the equations of dynamics has only been possible since the advent of computer calculation. However, the laws of conservation, quantity of movement, energy, kinetic moment, bring global constraints allowing a more direct understanding of certain phenomena.

1. Balancing forces

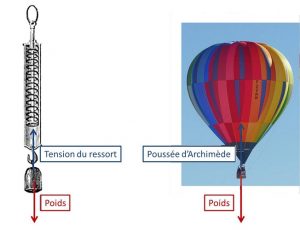
The notion of force expresses a mechanical action on an object. The forces have a well identified physical origin, for example the gravitational force (weight), the electrical force on a charged particle, the contact or tension force on a cable, or the elastic force of a spring. Like many fundamental notions of physics, force is difficult to define in itself, but it is approached through experimental examples as well as through the mathematical relationships it has with other quantities.

A force is thus characterized by its intensity (or modulus) and direction, as well as its point of application, and is mathematically represented by a vector. The sum of the forces acting on a resting object must cancel each other out. A force can be measured by the elongation of a spring from its rest position (Figure 1). Experimentally, it is verified that this elongation is proportional to the force by successively adding several identical weights. Once calibrated, this spring force gauge can be used to measure different forces. For a hot air balloon immobile in the air, the total weight is balanced by the Archimedes’ thrust, equal and opposite to the mass of the displaced air volume. This is none other than the result of the atmospheric pressure forces acting all around the envelope: due to the pressure decrease with altitude, the pressure is higher at the bottom of the envelope than at the top, which translates into a net upward force. This balance between pressure and force of gravity actually applies to any volume of fluid in equilibrium, known as hydrostatic equilibrium (see “Pressure, Temperature, Heat“). It is thanks to this balance that air plots, or water plots within a basin, do not fall to the ground under the influence of gravity. When the air is heated, its density and therefore the mass of a given volume decreases, while the pressure remains unchanged because it is controlled by the weight of the surrounding air. The balance is then disrupted leading to a vertical acceleration of the balloon. In the atmosphere, an air mass heated locally by solar radiation will also tend to rise: this is the principle of convection.

More generally, the balance of forces must be expressed as vectors, which is the basis for calculating structures in architecture, see Figure 2. For each material point, for example the intersection node of the wires, the vector sum of the forces must cancel each other out at equilibrium, as shown in Figure 3a. This makes it possible, for example, to find the intensities of forces _F1 and F2 knowing the force F3 and the angles _θ1 and _θ2, either by geometric construction or numerically by projecting the vectors along vertical and horizontal axes. An extended object, for example a solid, is described in physics as a set of material points held together by internal forces. These forces are to be distinguished from external forces such as weight or forces of contact with other objects. The sum of the internal forces is cancelled out by the principle of action and reaction, so that equilibrium requires the cancellation of the sum of the external forces.

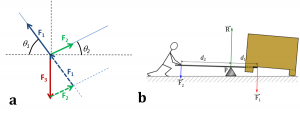
But the equilibrium condition of an extended object also requires the cancellation of the total moment of the forces, to avoid its rotation. The moment of a force with respect to an axis is defined as the product of the force, projected perpendicular to the axis, by the distance to the axis. The classic example is the lever shown in Figure 3b. At equilibrium, or quasi-equilibrium for a slow movement, the cancellation of moments requires that _F1d1 = F2d2 (the forces here being perpendicular to the axis) which makes it possible to amplify the force exerted in the inverse ratio of the distances to the axis (according to the usual convention we note here _F1 the intensity of the force while _F1 represents the force vector). It is usual to consider the moments in relation to the axis of the lever, because the moment of the reaction force R of the ground cancels itself out. However, the same result could be obtained by calculating the moment with respect to any mathematical axis, adding the moment of the reaction R, which is an equal vector and opposite to the sum of the two forces F1 and F2.

2. Forces and acceleration

Now leaving the domain of statics, the acceleration of an object is linked to the total force F which acts on it by the famous law of Newtonian dynamics, F = mg where m is the mass of the object and g its acceleration vector. This makes it possible to define the unit of force, the Newton (N), as the force producing an acceleration of 1 (m/s)/s over a mass of 1kg, which is written 1 N = 1 kg m s-2.

In the absence of force, an object moves at a uniform speed, this is the principle of inertia first stated by Galileo (1564-1642). This principle was not very intuitive at the time, because in everyday life any movement tends to stop in the absence of effort. This deceleration (negative acceleration) is now attributed to friction forces, which are opposed to speed. But friction becomes negligible in the interplanetary void, and Newton’s (1643-1727) great success was to mathematically describe the motion of planets and satellites from a simple law of universal gravitational force decreasing as the inverse of the square of the distance r.

The application of Newton’s law required the invention of the mathematical concept of a derivative specifying the notions of speed and acceleration. We note the speed v = dz/dt where dz is a small displacement in a time interval dt. In fact, we consider the limit of a very short time interval. Similarly, acceleration is noted as g = dv/dt. For a constant acceleration g, the velocity is proportional to time, v = gt, and it is easily demonstrated that the falling distance (difference between initial altitude z0 and altitude z) is then z0-z = (1/2) gt2. Thus on Earth under the action of gravity, g = 9.8 m s-2, an object reaches a speed of 9.8 m/s (35 km/h) in 1s, and falls from a height of 4.9 m.

Newton’s law applies more generally in vectorial form: the object can fall vertically as previously stated while retaining its horizontal velocity component by inertia. For a sufficiently high horizontal velocity, the curvature of the Earth must then be taken into account, and the circular motion of a satellite is obtained, see Figure 4. In this case the velocity is constant in modulus but the velocity vector rotates at the same angular velocity [1] as the satellite. The acceleration is then perpendicular to the velocity and directed towards the centre of the Earth, with the value g = v2/r, as shown in Figure 4. Thus for a satellite close [2] to the Earth, g = 9.8 ms-2, r = 6500 km, which leads to : speed v = (gr^)1/2 = 8 km/s, a revolution time (length 40 000 km) T = 5000 s (1 h 23 min).

This is what makes it possible to calculate the satellite velocity v=8000 m/s near the Earth’s surface (r=6500 km, g=9.81 ms-2). If now gravity g decreases in 1/r2, the velocity v = (gr^{)1/2 of} the circular motion decreases in 1/r1/2 and the period of revolution, equal to 2πr/v, increases in r3/2. Thus the Moon far from the Earth of r = 384 000 km, i. e. 60 times the Earth’s radius, must rotate in a time 465 times longer than a nearby satellite, i. e. 27 days. This is in line with the observations [3]. The law of growth of the time of revolution in r3/2 had been discovered by Kepler (1571-1630) for planets in orbit around the Sun. Beyond the particular case of the circular orbit, Newton was able to demonstrate that the general motion follows an ellipse (or hyperbola beyond the exhaust velocity), and he was able to find the three laws previously established by Kepler based on precise measurements of the positions of the planets.

It happens that the force of gravity itself is proportional to the mass, so that the acceleration produced is independent of it: all bodies fall with the same acceleration in the same place. This equivalence between heavy mass and inertial mass was stated by Galileo, and illustrated by his famous experiments (perhaps only imagined) of falling objects from the Tower of Pisa. This was done again with great precision in the vacuum, avoiding air friction. As a demonstration for the public, a film comparing the fall of a hammer and a feather was made on the Moon during the Apollo XV mission [4], and a similar experiment filmed on Earth in a huge vacuum chamber [5]. It is because of this principle of equivalence that all objects float in weightlessness in a satellite, each following exactly the same orbit around the Earth. This equivalence is now tested with a relative accuracy of 10-13 (1/10 trillion), and an accuracy of 10-15 is expected from the recently launched “Microscope” satellite. These ultra-precise measurements are intended to test deviations from the principle of equivalence predicted by new gravitational theories.

3. Kinetic and potential energy

In the example of the free fall mentioned above, it can be noted that mg(z0-z) = m(1/2)g2t2 = (1/2)mv2. This corresponds to the more general property of total energy conservation, composed of kinetic energy (1/2)mv2 and potential energy mgz. When an object falls, its kinetic energy increases, but its potential energy decreases as much, so that the total mechanical energy is preserved (in the absence of friction). In the general case, the kinetic energy (1/2)mv2 is expressed as a function of the velocity modulus. Mechanical energy conservation is becoming more common in the case of a satellite, but the expression of potential energy must then be modified to take into account the decrease in the force of gravity. This potential energy depends only on the position of the object, so that it finds the same value after a revolution, and the kinetic energy also finds the same value, in accordance with the fact that the planetary movement persists indefinitely. Gravity potential is defined by dividing this potential energy by the mass of the object. This potential characterizes the gravitational field independently of the object orbiting it (as long as the object is small and does not set the planet in motion by reaction).

The conservation of mechanical energy requires a particular form of the laws of force. Friction forces, unlike gravity, reduce mechanical energy, so that a satellite eventually falls into contact with the residual atmosphere. However, the mechanical energy lost is converted into heat so that the total energy remains preserved (read “Energy“). Heat essentially corresponds to the disordered kinetic energy of the gas molecules. For a homogeneous spherical planet, the potential varies in -1/r, so that the equipotentials are concentric spheres. However, these spheres are slightly deformed due to the Earth’s rotation and inhomogeneities. The equilibrium form of the ocean surface is such an equipotential (see “The marine environment“). Indeed, an object moving on an equipotential retains the same potential energy, and since its total energy is conserved, it cannot acquire (or lose) velocity under the effect of gravity alone. Conversely, if the shape of the ocean deviates from an equipotential, surface water tends to flow to regions of lower potential until it fills them and reaches the equilibrium state where the surface is equipotential. The surface of the solid Earth is also approaching equipotential due to erosion and plasticity of the Earth’s mantle.

4. Quantity of movement

The quantity of a movement of an elementary mass (considered as punctual) is defined as the product of mass and velocity, a definition that can be extended to any physical system by adding (vectorially) the quantities of movement of each of its elementary masses. It is easily demonstrated that the amount of movement is equal to the amount of movement of the centre of inertia (barycentre) of the system affected by its total mass. Newton’s law of dynamics then indicates that the time derivative of the amount of motion is equal to the sum of the forces acting on the system.

According to a fundamental principle of physics, the amount of movement of an isolated system is preserved. In other words, its centre of inertia moves in translation at a uniform speed, and only external forces can change this speed. Another equivalent formulation is the principle of action and reaction, which stipulates that any body A exerting a force on a body B undergoes a force of equal intensity, but in the opposite direction, exerted by the body B. The law of dynamics then indicates that these internal forces do not change the amount of movement of the global system A+B. This generalizes the static equilibrium condition discussed above.

Knowing the initial masses m1 and _m2 and initial velocities u1 and u2 of each mass, the amount of movement before the impact m1u1+m2u2 is calculated, which must be preserved after the impact, thus providing a constraint on the final velocities. If we further assume that the shock is elastic, i. e. that the kinetic energy (1/2)m1u12+(1/2)_m2u22 is retained, we can deduce the two final speeds. For two equal masses, we have an exchange of speeds (Figure 5a). In the case of a completely inelastic impact, the masses remain bound after the impact, with a final velocity equal to the weighted average of the initial velocities m1u1+m2u2/(m1+m2) by maintaining the amount of movement. Applied to the molecules of a gas, these shock properties make it possible to interpret the phenomenon of viscosity, which equalizes the quantities of movements of the fast and slow zones within the fluid, while preserving the total quantity of movement.

The propulsion of rockets or aircraft is another classic example: the amount of movement brought to the vehicle is just opposite to that of the ejected gas, regardless of the complex mechanisms involved. This also applies to the forces of gravity, the Moon attracting the Earth with a force equal to and opposite to the Earth’s force of gravity acting on the Moon. The Earth thus rotates around the centre of inertia of the Earth-Moon system in the same way as the hammer launcher, which must rotate to compensate for the reaction of the rotating ball (see “Tides“). It is this centre of inertia that describes the elliptical orbit around the Sun and not the Earth itself.

 

 

5. Angular momentum

The angular momentum with respect to an axis is defined for a point mass as the product of the distance to the axis by its amount of motion projected perpendicular to that axis. This definition is generalized to an extended body, for example a solid, by dividing it by thought into elementary masses, and adding their angular momenta. We demonstrate from the law of dynamics that the time derivative of the kinetic moment is equal to the total moment of the forces (also called “torque“) acting on the system. This generalizes the law of statics which requires that the total moment of the forces be zero.

The law of conservation of the kinetic moment stipulates that the total moment of the internal forces cancels out, and therefore only the moment of the external forces can change the kinetic moment. Thus in a solid state, the internal cohesion forces do not intervene in the balance of kinetic moment, just as they do not intervene in the amount of movement. It is a fundamental law of physics, distinct from and complementary to the principle of action and reaction.

In other words, a system cannot start rotating spontaneously nor lose its initial rotation without the action of external forces. However, its rotation speed may change in the event of contraction or extension. Indeed, for a point mass, it is the product of the velocity u by the distance r to the axis that is retained, so the velocity u increases in inverse proportion to the distance r, and its angular velocity u/r in inverse proportion to the square of this distance.

The classic example is that of the skater, and in natural environments, the formation of tornadoes and cyclones (see “Tornadoes: powerful devastating eddies“). The rotation of the Earth itself results from the amplification of the angular velocity during the accretion of the matter that led to its formation. The most spectacular example is pulsars, extremely dense stars rotating with a period of a few seconds to a few milliseconds. These objects result from the collapse of a massive star, typically passing from a radius of 1 million km to 10 km. Such a contraction increases the angular velocity of rotation by a factor of 10 billion (part of the angular momentum being ejected with the gas emitted by the explosion).

The angular momentum is in fact a vector, aligned with the axis of rotation [6], and it is therefore preserved both in direction and in modulus. This is the principle of the gyroscope. Similarly, the axis of rotation of the Earth remains aligned with respect to the stars, with the North Pole still pointing towards a region close to the North Star.

This is true only for an isolated system, and more precisely in the absence of torque (or moment) from external forces. A torque perpendicular to the axis of rotation produces a rotation of the axis of rotation, without any change in the angular velocity: this is the precessional phenomenon observed on a router, see Figure 6 (just as an acceleration perpendicular to the speed produces a rotation of the speed without changing its module). A similar effect occurs for the Earth because of its flattened shape at the pole: a torque results from the stronger lunar attraction on the part near the bead than on its opposite part. This leads to a slow precessional movement of the Earth’s rotation over a period of 26,000 years (see Figure 6). Thus the direction of the pole slowly moves over the celestial sphere over the centuries. This results in a displacement in the Earth’s orbit of the equinoxes’ position, when the Earth’s axis of rotation is oriented perpendicular to the direction of the Sun. This is why the phenomenon is called “precession of the equinoxes“. The associated variation in sunlight occurs in climate change between glacial and temperate periods.

 

---

References and notes

Cover photo. By http://creativecommons.org/licenses/by-sa/2.0 (Uploaded to Flickr as jfpds regular)[CC BY-SA 2.0 (极博双板滑雪俱乐部)], via Wikimedia Commons.

[1] The angular velocity Ω is the angle travelled per unit of time, generally expressed in radian/s, so that Ω=v/r . A radian is defined as the angle intercepting an arc of a circle equal to the radius, so that the complete revolution (circumference 2πr) represents 2π radian, and the period of revolution is T=2π/Ω=2πr/v.

[2] The altitude must be a few hundred kilometres to avoid atmospheric friction, but the acceleration of gravity remains close to that of the Earth’s surface, and the radius of the orbit is little different from that of the Earth.

[3] This is the sideral revolution, i. e. with respect to the stars, while the time between two full moons, of 29.5 days, is the synodic revolution, i. e. with respect to the Sun.

[4] Apollo 15 Hammer and Feather Drop- Youtube

[5] Brian Cox visits the world’s biggest vacuum chamber – Human Universe: Episode 4 Preview – BBC Two – Youtube

[6] The angular momentum is more precisely defined in relation to an origin point O. For a point mass m at point M it is the vector product of the vector OM by the amount of motion mu of the mass at point M. For an axisymmetric solid such as a router or the Earth, the kinetic moment is aligned on the axis of rotation, with a value proportional to the angular velocity and the moment of inertia.