Les marées
PDF
La marée désigne le processus de variation périodique du niveau de la mer, en général semi-diurne (période proche de 12h), mais diurne dans certaines régions. La marée est due à l’attraction lunaire, et dans une moindre mesure à l’attraction du Soleil qui module son amplitude selon la phase de la Lune et différentes périodes astronomiques. Des courants par endroit très violents sont associés aux marées dans les zones côtières. Les courants de marée jouent par ailleurs un rôle global sur le climat en contribuant au mélange vertical de l’océan, qui refroidit la surface par le contact avec l’eau profonde. Enfin à l’échelle des temps géologiques, la marée ralentit la rotation terrestre et éloigne la Lune de la Terre.
1. Des observations depuis l’antiquité
Les liens entre marée et mouvement de la Lune sont connus empiriquement depuis l’antiquité [1]. Le moment de la basse mer (marée basse) et de la pleine mer (marée haute) retarde d’environ 25 minutes par marée. Ce retard de 1/60 jour correspond au déplacement de la Lune sur son orbite de 1/60 tour en 12 h. A cause de ce retard la période effective de marée est de 12 h 25 mn.
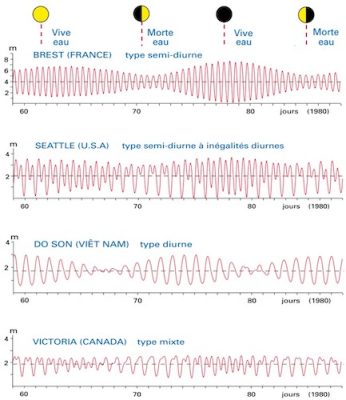
On sait aussi que les marées sont plus intenses pendant la pleine et la nouvelle Lune (vives eaux) que pendant les premiers et derniers quartiers (mortes eaux), comme on peut le voir sur la première courbe de la Figure 1, montrant la hauteur d’eau enregistrée à Brest. Ceci indique que le Soleil contribue aux marées. La marée est particulièrement forte aux équinoxes et dépend aussi de la distance de la Lune qui varie d’environ 10 % à cause de son orbite elliptique. L’amplitude de marée en un lieu donné est ainsi modulée par un coefficient de marée qui varie de 20 à 120 selon les différentes périodes astronomiques.
En raison de son élasticité, la Terre solide est également soumise à un effet de marée mais avec une amplitude moindre, de quelques dizaines de cm. Ce que l’on observe en bord de mer est la différence entre la marée océanique et cette marée terrestre. Les mesures anciennes étaient réalisées près du rivage par des marégraphes à flotteur, plus récemment remplacés par des détecteurs de niveau d’eau par ultrasons ou radar. Les satellites altimétriques permettent maintenant de cartographier la marée sur l’ensemble de la surface océanique par mesure radar, après calibration par des bouées dont la position est repérée par GPS.
2. Théorie statique de Newton
Les marées ont été très tôt interprétées comme un effet d’attraction de la Lune et du Soleil. Cependant ces explications butaient sur le fait que la mer est soulevée non seulement du côté de la Lune, mais aussi du côté opposé, conduisant à la période principale de 12h (plutôt que 24 h). C’est Isaac Newton (1643-1727) qui a le premier compris ce paradoxe grâce à sa théorie de la gravitation universelle publiée en 1687 dans son fameux ouvrage Philosophiae Naturalis Principia [3]. Les marées y tiennent une place importante car c’était à cette époque l’effet le plus tangible de l’attraction par un corps extérieur à la Terre.
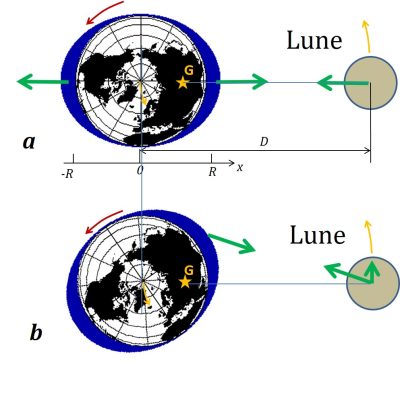
Newton a tout d’abord compris que si la Terre maintient la Lune en orbite par sa force d’attraction, la Lune doit en retour exercer une force égale et opposée sur la Terre : c’est le principe de l’action et de la réaction. Ainsi la Terre tourne un peu autour de la Lune, plus précisément autour de leur barycentre commun (point G sur la Figure 2). Tout corps sur la Terre l’accompagne dans son mouvement autour de ce barycentre, de la même façon qu’un cosmonaute en orbite reste en apesanteur près de son vaisseau spatial. En effet tout corps subit la même accélération dans un champ de pesanteur quelle que soit sa masse. Ce qui va déplacer l’océan par rapport à la Terre est donc non pas le champ d’attraction principal de la Lune, mais la différence entre ce champ et celui agissant au centre de la Terre. Un excès d‘attraction s’exerce au plus près de la Lune et un défaut d’attraction du côté opposé plus éloigné, produisant un bourrelet de chaque côté, comme montré sur la Figure 2. Un autre argument équivalent consiste à se placer dans un repère tournant autour de ce barycentre à la vitesse angulaire orbitale de la Lune: la force centrifuge compense alors l’attraction lunaire au centre de la Terre, mais elle domine au point opposé à la Lune, tandis que l’attraction domine du côté de la Lune. Ceci conduit respectivement aux deux bourrelets.
Dans la théorie dite statique proposée par Newton, ce bourrelet est supposé fixe par rapport au système Terre-Lune. Au cours de sa rotation autour de la Terre, un point passe ainsi successivement par chaque bourrelet conduisant à deux marées hautes par jour, d’où la période semi diurne.
L’effet du Soleil vient s’ajouter à celui de la Lune lorsqu’il est dans la même direction (nouvelle Lune), mais aussi lorsqu’il est en direction opposée (pleine Lune), du fait du double bourrelet. Ceci explique l’alternance observée entre marées de vives eaux et mortes eaux. La force d’attraction du Soleil est plus forte que celle de la Lune, mais la différence entre les deux côtés plus faible en raison de la grande distance, produisant un effet de marée inférieur. Ainsi la force d’attraction gravitationnelle décroit comme le carré de la distance tandis que l’effet de marée correspondant décroit comme le cube de la distance.
3. Variations d’amplitude de la marée
Une complication est apportée par le fait que ces différentes rotations s’effectuent selon des axes différents : l’axe de rotation terrestre est incliné de 23°26’ par rapport au plan de l’orbite terrestre, lui-même proche du plan de l’orbite lunaire (incliné de 5° 9′ par rapport au plan de l’orbite terrestre). Le schéma de la Figure 2 s’applique strictement aux équinoxes, quand l’axe de rotation est bien transverse à la direction du Soleil, aligné avec la Lune au moment des vives eaux.
Cependant aux solstices, un point de la Terre parcourt les bourrelets selon un cercle incliné, conduisant à une plus faible amplitude. On peut s’en convaincre en considérant le cas limite d’une inclinaison à 90° : au solstice l’axe de la Terre serait alors orienté le long de l’axe du bourrelet, et un point sur Terre tournerait alors autour sans variation de hauteur, à la manière d’un ballon de rugby en rotation autour de son grand axe.
Enfin l’orbite de la Lune n’est pas circulaire, mais elliptique, de sorte que sa distance à la Terre varie de 10% entre le périhélie (minimum) et l’aphélie (maximum). Il s’en suit que l’effet de marée est plus grand au périhélie de 30% (à cause de la dépendance en cube de la distance). Ces différents effets astronomiques sont pris en compte de façon très précise pour établir les tables de marée. La compréhension et la prédiction des marées ont suscité de très nombreux travaux tout au long des 19e et 20e siècle (focus 1) en raison de son intérêt fondamental et de son importance pour la navigation et pour l’utilisation du littoral.
4. Ondes de marée
Le schéma statique de Newton suppose que le bourrelet océanique, fixe par rapport à la Lune, se propage donc par rapport à la Terre à la vitesse opposée à sa rotation, soit 450 m/s à l’équateur. Ceci n’est pas possible car une déformation de la surface de l’océan se propage à une vitesse limitée à environ 200 m/s. Cette vitesse est liée à la profondeur d et l’accélération de la gravité g par la formule c=(gd)1/2 (lire https://www.encyclopedie-environnement.org/eau/vagues-houles/), ce qui conduit en effet à c=200 m/s pour une profondeur moyenne de d=4000 m. Cette onde se trouve donc en retard par rapport à la position de la Lune, ce qui conduit à un décalage en retard du bourrelet comme schématisé sur la Figure 2b.
La forme des côtes contraint aussi fortement la propagation, les bassins océaniques se comportant comme de grandes cuvettes d’eau secouées par la force de marée. Il s’y établit des modes propres d’oscillation, analogues aux modes de vibration des ondes sonores dans un instrument de musique.
La théorie de Newton reste exacte en tant que force motrice mais la déformation qui en résulte dépend donc de ces phénomènes de propagation et des résonances qui apparaissent lorsque la fréquence d’excitation coïncide avec des fréquences propres d’oscillation des bassins océaniques.
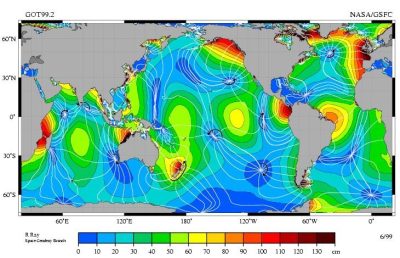
L’amplitude des marées est maintenant cartographiée avec une précision de l’ordre du centimètre grâce aux satellites altimétriques (voir Figure 3). On voit que l’amplitude est très variable, au gré des ventres d’oscillation (maxima en rouge) et des nœuds d’oscillation ou l’amplitude s’annule (en bleu). Les lignes d’égale phase sont également montrées : elles représentent le retard du maximum de marée par rapport au passage de la Lune au zénith. L’onde de marée se propage perpendiculairement à ces lignes, donc en tournant autour des nœuds. Cette rotation, due à la force de Coriolis, est dans le sens contraire aux aiguilles d’une montre dans l’hémisphère Nord.
La modulation des marées par les différents effets astronomiques s’exprime plus précisément comme une somme d’excitations à des périodes différentes, le mode semi-diurne étant cependant dominant. C’est ce mode, appelé M2, qui est représenté sur la Figure 3. On remarquera que la distance moyenne entre ventres (ou entre noeuds) correspond à la longueur d’onde de marée de l’ordre de 8500 km, soit la distance parcourue par l’onde à la vitesse c=200 m/s pendant la période de 12 h.
Il existe aussi une excitation à la période diurne, résultant d’une légère asymétrie des deux bourrelets d’attraction opposés. Ce mode appelé M1 est forcé à un niveau 20 fois plus faible que le mode M2, mais il entre efficacement en résonance avec l’océan Pacifique, de taille comparable à sa longueur d’onde, environ 15 000 km. La marée diurne est ainsi importante dans certaines régions du Pacifique. Les régions situées sur des noeuds du mode M2, comme le Viet-Nam, voient alors essentiellement ce mode M1 (3e courbe de la Figure 1). D’autres régions présentent une superposition des deux modes M1 et M2 (2e et 4e courbes de la Figure 1).

L’onde de marée est souvent amplifiée dans les baies ou mers intérieures comme la Manche. En effet l’énergie s’y propage moins vite, en racine carré de la profondeur, d’où une augmentation de densité d’énergie à flux constant: passer de 5000 m à 50 m produit ainsi une augmentation d’énergie d’un facteur 10, soit une augmentation de l’amplitude d’un facteur 3. Ainsi dans la Manche, l’amplitude moyenne passe typiquement de 1 m au large à 3 m, et la marée est associée à un fort courant. Le courant entrant est dévié vers la côte Française par la force de Coriolis, et s’en écarte au contraire à marée descendante, ce qui amplifie l’amplitude de marée du côté Français, au détriment du côté Anglais. Ces effets ont pu être reproduits en similitude sur la grande plate-forme tournante « Coriolis », montrée sur la figure 4. Le forçage par la marée océanique est alors reproduit par un batteur oscillant situé à l’entrée de la Manche. L’amplitude est la phase de la marée sur l’ensemble de la Manche ont ainsi pu être reproduits (Figure 5).
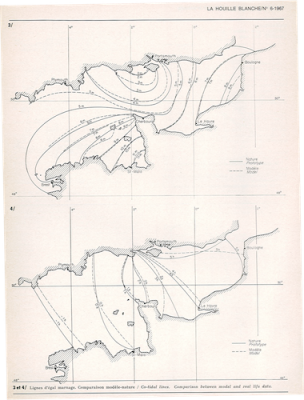
Les modèles numériques actuels permettent de reproduire et de prédire ces phénomènes de marée avec une précision de l’ordre de 1 cm en prenant en compte l’excitation et la propagation de tous ces modes. Les principales difficultés sont la prise en compte du frottement sur le fond océanique en régime turbulent et les pertes d’énergie par excitation de marée interne (voir section 7).
5. Autres influences sur le niveau de la mer
La marée n’est pas le seul effet influençant le niveau de la mer. On peut tout d’abord se poser la question de la pertinence de mesures au cm près dans une mer souvent agitée de vagues de plusieurs mètres. Mais le niveau moyenné sur plusieurs km carrés est très bien défini même s’il fluctue très fortement en chaque point. De plus, en ce qui concerne les amplitudes de marée comme celles de la Figure 3, le signal est filtré à une période donnée (12h 25 min), à la manière de la sélection de fréquence utilisée pour capter les ondes radio. Ainsi les effets agissant à d’autres fréquences ne sont pas pris en compte.
Parmi ces autres effets, la pression atmosphérique est un facteur assez immédiat. Une haute pression fait localement baisser le niveau de l’eau : une surpression de 10 hPa = 103 N/m2 induit par simple équilibre hydrostatique une baisse du niveau de 10 cm (la hauteur h d’une colonne d’eau dont le poids ρgh est de 103 N/m2 (ρ≈103 kg/m3 représente ici la densité de l’eau). Une basse pression fait au contraire monter le niveau. La surcote atteint une valeur de un mètre pour une pression atmosphérique de 913 hPa, se produisant au cœur d’ouragans extrêmes. Cette montée des eaux amplifie les dégâts dus aux vagues et aux fortes précipitations dans les régions côtières.
Un deuxième effet, dynamique cette fois, est dû à la force de friction du vent. Lorsque celui-ci est dirigé vers le large, cette force abaisse le niveau d’eau, et au contraire pousse l’eau vers le rivage dans le cas contraire. Une surélévation de l’ordre de 1 m peut être ainsi produite lors de fortes tempêtes. La coïncidence de ces phénomènes avec de fortes marées favorise la rupture de digues de protection à l’origine d’inondations comme lors de la tempête ‘Xynthia’ qui frappa la France en Février 2010, ou l’ouragan Katrina qui inonda la Nouvelle-Orléans en Aout 2005. Ces phénomènes, dépendant des vents et pression, sont cependant plus prévisibles que les précipitations intenses et très locales à l’origine des inondations éclairs.
A plus long terme, le niveau moyen de la mer croit en présence de réchauffement climatique en raison de la dilatation de l’océan, pour 65 % environ, et de la fonte des glaciers pour les 35% complémentaires. Les mesures récentes indiquent une élévation moyenne de l’ordre de 2 mm/an.
Enfin le niveau de l’eau sur le littoral dépend aussi de l’évolution de la Terre solide. Le transport de sédiment modifie le trait de côte, par envasement ou érosion. Ce dernier effet tend actuellement à dominer en raison des barrages sur les grands fleuves qui réduisent l’apport de sédiments. La côte de Louisiane est ainsi fortement érodée à cause de la baisse des sédiments apportés par le Mississippi. Les mouvements géologiques profonds apportent également leur contribution, modifiant la forme des côtes par la dérive des continents sur des durées de millions d’années. Au Canada et en Europe du Nord, l’effet géologique le plus marquant est le rebond post-glaciaire qui soulève la Scandinavie de plusieurs mm par an suite à l’allégement dû à la fonte des calottes glaciaires survenue il y a 10 000 ans. Ce soulèvement induit par compensation un enfoncement des zones périphériques comme la Bretagne. Ainsi des menhirs dressés sur la Terre ferme il y a 7000 ans se retrouvent dans la mer, après un enfoncement du continent d’environ 7 m.
6. Exploiter l’énergie de la marée
Les moulins à marée ont été utilisés depuis le Moyen Age pour capter l’énergie de la marée sur les sites favorables, les estuaires ou anses à l’abri des vagues pouvant être équipés de petits barrages. Le principe en a été repris pour l’usine marémotrice de la Rance, mise en service en 1967. Avec une puissance moyenne de 57 MW (puissance installée de 240 MW), elle produit 3,5 % de la consommation électrique de la Bretagne (et 45% de sa production électrique). Elle est restée la plus grande usine marémotrice au monde pendant 45 ans, jusqu’à la mise en service en 2011 de la centrale de Sihwa Lake en Corée du Sud, légèrement plus puissante (254 MW installé). L’installation utilise un barrage en travers de l’estuaire de la Rance, avec turbines à pales orientables pouvant fonctionner dans les deux sens, à marée montante ou marée descendante.
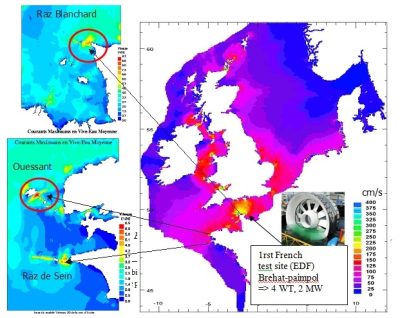
Cependant peu de sites à forte marée permettent la construction d’installations de cette taille, et les impératifs de préservation des sites naturels rend aujourd’hui difficile leur construction en bord de mer. Un projet beaucoup plus ambitieux consistait à barrer la baie du Mont Saint-Michel, site particulièrement exceptionnel en termes d’amplitude de marée. Ce projet a ensuite été abandonné au profit du développement des centrales nucléaires dans les années 1970.
Cette ressource représente à peine 0,2 % de la puissance totale dissipée pas les marées et donc perdue par la rotation terrestre (voir section 8). L’extraction d’énergie tend à freiner le courant de marée et donc à réduire localement son amplitude, ce qui réduit les pertes par frottement visqueux. On peut s’attendre à ce que l’énergie extraite soit de toute façon dissipée en chaleur en l’absence de captage. Il n’est cependant pas facile de calculer l’impact en retour sur la rotation terrestre, de toute façon très faible [6].
7. Marée interne
La densité de l’océan croît avec la profondeur, l’eau de surface étant plus chaude (donc moins dense) que l’eau profonde. Une telle stratification en densité peut également résulter de la salinité, par exemple au Détroit de Gibraltar où l’eau océanique pénètre dans la Méditerranée en restant en surface à cause de sa densité inférieure. On peut schématiser cette situation par un modèle à deux couches de densité différente.
Des oscillations dites ondes internes, peuvent se propager le long de cette interface de façon analogue aux ondes de surface. Elles sont cependant beaucoup plus lentes, décrites en remplaçant la gravité g par une gravité réduite gδρ/ρ, où δρ/ρ est la différence relative de densité entre les deux couches. Dans une couche de surface d’épaisseur H, la vitesse de propagation des ondes est donc c=(Hgδρ/ρ)1/2 . Pour une valeur typique δρ/ρ=0,001, la propagation est donc 30 fois plus lente que pour les ondes de surface d’une couche de même épaisseur : c=1 m/s pour une couche d’épaisseur H=100 m.

La génération de marée interne est observée dans de nombreuses régions de l’océan. L’une des plus actives est le Détroit de Luzon, séparant Taïwan et les Philippines, où une crête sous-marine engendre en Mer de Chine des ondes internes dont le déplacement vertical dépasse 300 m. La dissipation de ces ondes par déferlement contribue au mélange vertical de l’océan qui lui-même influe sur sa circulation générale et sur le climat.
8. Effets astronomiques et dissipation d’énergie
Sur des temps astronomiques, les marées ont pour effet d’augmenter la durée du jour, de 2 ms par siècle, soit environ une heure sur 200 millions d’années. Ce ralentissement de la rotation terrestre se mesure très bien avec les horloges atomiques actuelles. Par ailleurs l’effet de marée éloigne la Lune de 3,8 cm/an. Cet effet se mesure directement avec une précision de 1 cm en mesurant le temps d’aller-retour d’impulsions laser envoyées sur des réflecteurs déposés par les missions lunaires Apollo [7].
Le ralentissement de la rotation est confirmé par l’observation de coraux fossiles [8], dont les cercles de croissance journaliers permettent de compter les jours dans une année. Ainsi l’année comptait 410 jours il y a 400 millions d’années, soit une durée du jour de 21,5 heures. Des bandes mensuelles associées à la pleine Lune indiquent de plus que l’année comptait 13 mois. La Lune tournait ainsi plus rapidement (et était donc plus proche de la Terre).
Ces effets se comprennent facilement avec le schéma de la figure 2b. La rotation Terrestre tend à entrainer le bourrelet qui est donc déphasé par rapport au modèle statique de Newton. L’attraction lunaire exerce ainsi un couple qui ralentit la Terre et réciproquement apporte de l’énergie à la Lune. De façon contre-intuitive de prime abord, un tel apport d’énergie tend à éloigner la Lune, et donc à ralentir sa rotation, dont la vitesse décroit en 1/r1/2. Cependant le moment cinétique de la Lune, produit de la vitesse par la distance r à la Terre augmente bien (en r1/2), conformément au sens moteur du couple. Le moment cinétique de la Terre diminue dans la même proportion de sorte que le moment cinétique total est conservé. L’énergie mécanique totale diminue quant à elle, convertie en chaleur lors de la dissipation des courants marins produits par la marée.
Les mesures astronomiques permettent de déterminer avec précision la décroissance d’énergie de rotation et donc d’en déduire la puissance totale dissipée par les marées : 2,9 x 1012 watts. Les océanographes ont de leur côté estimé une puissance dissipée environ moitié par l’étude des courants de marée, majoritairement actifs dans les zones côtières. Il est maintenant établi que la ‘dissipation manquante’ est due à l’excitation de la marée interne (voir section 7), qui se propage à l’intérieur de l’océan et finit par se dissiper. Cette dissipation se produit par déferlement des ondes, produisant un lent mélange vertical de l’océan. L’influence de ces effets sur la circulation thermo-haline est actuellement l’objet d’actives recherches.
Notes et références
Image de couverture. Mont-Saint Michel, où les marées peuvent atteindre un marnage de 15m. source https://upload.wikimedia.org/wikipedia/commons/thumb/2/29/Mont-Saint-Michel_Drone.jpg/1280px-Mont-Saint-Michel_Drone.jpg .
[1] http://www.imcce.fr/promenade/pages5/525.html#Para02
[2] Les enregistrements de marée sur plus de 900 sites à travers le monde sont disponibles sur http://www.ioc-sealevelmonitoring.org/
[3] Newton I. (1687) ’Philosophiae naturalis principia mathematica’
[4] http://science.nasa.gov/media/medialibrary/2000/06/15/ast15jun_2_resources/oceantides.gif
[5] Maitre T., http://encyclopedie-energie.org/notices/les-hydroliennes
[6] Cette affirmation mériterait cependant d’être nuancée, car un captage important modifierait en retour la forme et la phase des marées, et donc le couple exercé sur la Terre. Quoique il en soit une extraction de 5 000 MW représente tout juste 0,2 % de la puissance totale dissipée dans les marées (voir section 8)
[7] http://culturesciencesphysique.ens-lyon.fr/ressource/laser-distance-terre-lune.xml
[8] Runcorn S.K. , « Corals as paleontological clocks», Scientific American, vol. 215, 1966, p. 26–33
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : SOMMERIA Joël (19 octobre 2021), Les marées, Encyclopédie de l’Environnement. Consulté le 27 juillet 2024 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/eau/les-marees/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.







