| Focus 1/1 | Atmospheric halos

Deviation of light by a prism

PDF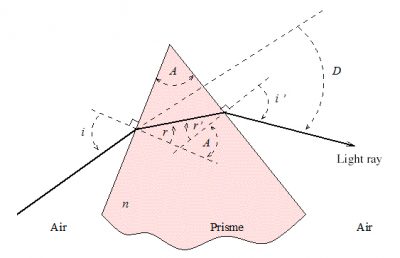
Figure 1. Deviation of a light beam by a prism of angle at vertex A and refractive index n.

A prism of angle at the apex A and index n – the air, of unit index, surrounds the prism – deflects a light beam, whose angle of incidence on one of the lateral surfaces of the prism is i, according to the laws of Snell-Descartes of geometric optics: sin i = n sin r and n sin r’ = sin i’ (Figure 1 for the notations). The angle of deflection D = i + i’ – A, with A = r + r’.

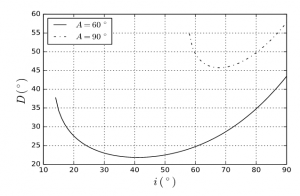
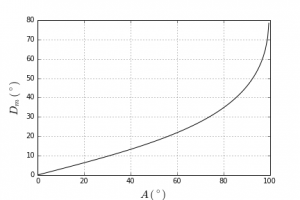
The light beam can only emerge from the prism if A < 2 a sin(1/n) ; for ice n = 1.31, hence A < 99.5⁰. If we trace the deviation D as a function of i, we see that it decreases rapidly, reaches a minimum minimorum corresponding to a symmetrical crossing of the prism (i = i’), then increases slowly. The minimum is very flattened, so that a change in the angle of incidence around the incidence that corresponds to this minimum does not significantly change its value; it results in an accumulation of light and therefore a high luminosity around this minimum. For A = 60⁰, the minimum is 22⁰; if A = 90⁰, it is 46⁰ (Figure 2). Figure 3 shows the value of this minimum for the different values of A allowed: it increases with A.

Encyclopédie environnement - prisme - déviation de la lumière en fonction de l'angle d'incidence
Figure 2. Deviation D as a function of the angle of incidence i on a prism of angle A = 60⁰ and angle A = 90⁰.
Encyclopédie environnement - prisme - Déviation miimale en fonction de l'angle
Figure 3. Minimum deviation Dm as a function of the angle A of a prism.
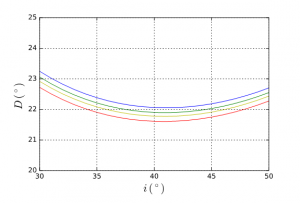
Encyclopédie environnement - prisme - déviation en fonction de la couleur de la lumière
Figure 4. Deviation D for an angle prism A = 60⁰ depending on the colour of the incident light. Each of the four curves is colored according to the color it represents.

In addition, since the index n depends on the colour of the incident radiation, the minimum also depends on it; a prism breaks down white light into its various monochromatic components. This explains the iridescence of halos obtained by refraction. For A = 60⁰, we have a minimum close to 22⁰ that grows from red to blue (Figure 4).

 

 

References and notes

Cover image. [Source: iwannt via VisualHunt.com / CC BY]

Registering

Registering