Planck’s theory

All attempts to explain the behaviour of the spectral density ρ_ν(ν,T) (shown in Figure 2 of the article) with the concepts of classical physics have failed. The theory is most easily derived in the particular case of an empty cubic cavity, with perfectly reflective walls, of unit volume. A phenomenon of standing waves similar to that of a vibrating rope fixed at its two ends then occurs. In a cavity, a mode characterizes a particular stationary electromagnetic wave given by its frequency ν, its propagation speed (or celerity) c, its propagation direction, and by the direction and amplitude of its electric field. The possible frequencies are discrete and are referred to as normal frequencies. The latter form a dense set of modes characterized by a density (number of modes per unit volume of the cavity) D(ν) proportional to ν².

In classical physics, the average energy < E(ν)> of a standing wave comparable to a harmonic oscillator [1] is simply k_BT where k_B is the Boltzmann constant and T the absolute temperature. This expresses the fact that at thermal equilibrium the energy is distributed evenly in all accessible modes. The energy spectral density ρ_ν(ν,T), given by the product D(ν)< E(ν)>, is then proportional to k_BTν². This result of classical physics, represented by the dotted line in Figure 2, is called Rayleigh’s model. By integrating over all frequencies from 0 to ν, it leads to a total energy density ρ proportional to k_BTν³. It grows without limit at high frequency ν leading to an infinite total energy, therefore unacceptable. This the so-called “ultraviolet catastrophe” led Max Planck to formulate his quantum hypothesis mentioned above.

The energy of a mode is quantized: the only possible energy values of a frequency mode are E_n=nhν, where n is a positive or zero integer and h  the Planck constant, which is identical for all oscillators. An oscillator in an energy state E_n is equivalent to n quanta or photons of energy hν. The energy exchanges between the wave and matter (atoms, molecules) are thus carried out in a discrete way by exchanging photons. By quantifying the energy of each oscillator in this way, a statistical calculation [2] [3] shows that the average energy of each oscillator is now given by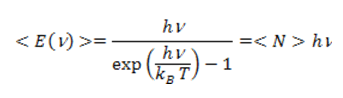where < N> is the average number of photons of the mode with energy hν at temperature T. For low-frequency modes (hν small in front of k_BT), this expression reduces to the classical law < E>=k_BT. These modes contain many photons. However the energy of the modes drops exponentially as h_ν clearly exceeds k_BT, and < N> becomes much smaller than 1. By multiplying the mean energy of the modes by their density D(ν), we obtain the famous Planck formula :

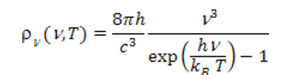where c is the speed of light in vacuum. The variation of ρ_ν(ν,T) as a function of frequency ν has been shown in Figure 2 for various temperatures. This formula is in remarkable agreement with experiences. It also allows to experimentally determine the two constants h/c³ and h/k_B from which the value of the Planck constant h = 6.62617 x 10^-34 Js and the Boltzmann constant k_B = 1.38066 x 10^-23 J/K is derived. This leads to an unexpected evaluation of the Avogadro number N_A=R/k_B=6.0221 x10²³ mol^-1 , in excellent agreement with its value obtained by other methods (R is the constant of perfect gases, read  pressure, temperature, heat).

By integrating on all frequencies we obtain the energy density of the black body ρ = αT⁴ as well as the radiated Φ flux per unit area of the black body given by Stefan-Boltzmann’s law Φ=σT⁴, with σ=2π⁵k_B⁴/(15c²h³). This leads to results that are remarkably in line with experience. Note that if we express the spectral energy density as a function of wavelength, Planck’s theory leads to [4]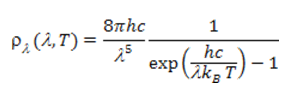The curves in Figures 4 and 5 are representative of this function and Wien’s law results from the position of its maximum.

This Planck’s theory published in 1901 was the first step towards the quantification of light, further confirmed by Einstein in 1905 who explicitly introduced the notion of photon to explain the photoelectric effect. The existence of energy levels in atoms and molecules was then proposed by Niels Bohr in 1913 to explain the line spectra. These results were later incorporated in the wider Quantum Mechanics theory which governs all microscopic phenomena. This formalism was gradually developed in the 1920s, with contributions from Louis De Broglie, Erwin Schrödinger and Werner Heisenberg.

References and notes

[1] Each mode is characterized by a solution of the type E_z = E₀ cos(ω t)sink_xx, where z is the direction of the electric field E, ω = 2πν is the pulsation of the wave and k_x = 2π/λ is the wave vector along the propagation direction x. A solution of this type is similar to that of a mechanical oscillator: a mass m suspended on a spring whose restoring force is proportional to the elongation x and whose movement is described by a harmonic oscillation of the form x = x₀ cos ωt.

[2] Elie Belorizky, Initiation to Quantum Mechanics, Dunod, Paris, 2003.

[3] Elie Belorizky, Introduction to Statistical Mechanics, Presse Universitaire de Grenoble, Grenoble sciences collection, 1992.

[4] We have the correspondence ν=c/λ and the equality of the energy densities : ρ_λ(λ,T) |dλ|= ρ_ν(ν,T) |dν|, which leads to ρ_λ(λ,T) = ρ_ν(ν,T) |dν/ dλ| = ρ_ν(c/λ,T)  c/λ².