Le rayonnement thermique du corps noir
PDF
Pourquoi la couleur d’un métal change-t-elle lorsqu’il est chauffé ? Comment peut-on déterminer la température d’une source lumineuse comme une lampe à filament de tungstène ou celle de la surface du soleil ou des étoiles ? Quelle est la température de l’Univers ? Quel est le principe d’une caméra thermographique ? Les réponses à ces questions se font par l’analyse du rayonnement d’un corps noir, c’est–à-dire d’un corps qui absorbe toute la lumière qu’il reçoit. La théorie de Planck qui explique ce rayonnement a été le premier pas vers le développement de la mécanique quantique.
1. Les différents types de rayonnement
Il existe plusieurs types de rayonnement c’est-à-dire d’émission d’ondes. On peut citer :
- Les ondes sonores émises par une personne qui parle, un instrument de musique ou un haut-parleur, la grandeur vibrante qui se propage avec l’onde étant alors la pression.
- Les ondes sismiques qui sont des ondes élastiques qui peuvent traverser un milieu en le modifiant selon l’intensité du séisme.
- Les ondes électromagnétiques qui, comme leur nom l’indique sont caractérisées par un champ électrique E et un champ magnétique B qui vibrent avec une certaine fréquence. Ces champs sont perpendiculaires entre eux et perpendiculaires à la direction de propagation des ondes.
Dans l’article la couleur du ciel , les ondes électromagnétiques ont été décrites de manière détaillée. Une onde électromagnétique particulière se propageant dans un milieu donné est caractérisée par sa fréquence ν, l’amplitude et la direction de son champ électrique, sa vitesse de propagation (ou célérité) V dans le milieu considéré. Dans le vide cette vitesse est c ≃ 300 000 km s-1. La longueur d’onde est λ = V/ν : c’est la distance parcourue par l’onde à la vitesse V pendant une période T = 1/ν. La fréquence est exprimée en hertz (Hz), c’est-à-dire en périodes/seconde noté plus simplement s-1. L’intensité d’une onde électromagnétique est proportionnelle au carré de l’amplitude de son champ électrique. Elle représente le flux d’énergie transporté par l’onde. L’orientation du champ électrique, lorsqu’elle est fixée, est sa polarisation.
On classe les différentes ondes électromagnétiques selon leur fréquence ν, ou de façon équivalente selon leur longueur d’onde dans le vide λ = c/ν. La gamme de longueurs d’onde est très étendue : de 103 m pour les grandes ondes radio à 10-12 m pour les rayons γ. Le spectre visible par notre œil est limité aux longueurs d’onde comprises entre 0,4 µm pour le violet et 0,8 µm pour le rouge (1 µm=1/1000 mm).
Les ondes électromagnétiques sont créées par des oscillations rapides de charges électriques. Les ondes radio (λ ~ 100 m), de télévision (λ ~ 10 m), celles utilisées par la téléphonie mobile et la WIFI (Wireless Fidelity, λ ~ 0,10 m), sont ainsi émises par des antennes parcourues par des courants électriques excitateurs. Les longueurs plus courtes, notamment les rayons X (λ ~ 10-10 m), peuvent soit être obtenues en accélérant ou en freinant des électrons dans le vide à différentes énergies, soit être émises par des atomes préalablement excités. Les rayons γ résultent quant à eux de réactions nucléaires (lire La radioactivité).
Les atomes ou les molécules d’un gaz excités par un apport d’énergie émettent un rayonnement électromagnétique à des longueurs d’onde précises caractéristiques de la nature du gaz (c’est ainsi que l’on connait la composition chimique de la surface des étoiles). C’est ce qu’on appelle un spectre de raies. Il existe aussi un rayonnement dit thermique, que tout corps émet du seul fait de sa température. Ce rayonnement se répartit sur une gamme continue de longueurs d’ondes, ce qu’on appelle un spectre continu. C’est le cas d’une lampe d’éclairage à filament, du Soleil ou des étoiles et plus généralement de la surface d’un corps chauffé à une certaine température. Pour analyser ce rayonnement il faut étudier les propriétés du corps noir défini dans le paragraphe suivant.
2. Le rayonnement interne du corps noir
Un corps noir est un objet idéal qui absorberait toute l’énergie électromagnétique qu’il recevrait, sans en réfléchir ni en transmettre. Ainsi éclairé, il absorberait totalement la lumière et devrait apparaître noir, d’où son nom. Cependant il n’apparait noir qu’à basse température, car il émet de la lumière d’autant plus que sa température est élevée ; c’est ce phénomène qui est décrit ici.
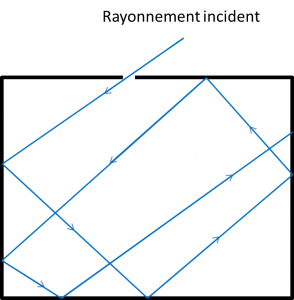
Un corps noir est bien représenté par un petit trou percé dans une cavité portée à une température absolue T (par exemple un four). Le trou doit être suffisamment petit pour ne pas perturber l’équilibre dans la cavité (Figure 1). En effet, si le trou dans la paroi est assez petit, tout rayonnement provenant de l’extérieur et pénétrant dans la cavité se réfléchit plusieurs fois sur les parois et a une probabilité très faible de ressortir par le trou. On peut alors analyser expérimentalement le rayonnement du trou vers l’extérieur en fonction de la fréquence ν des ondes émises et de la température T des parois de la cavité.
Dans cette cavité, vide de tout gaz pour simplifier, les atomes composant les parois émettent de façon permanente un rayonnement électromagnétique et absorbent celui émis par les autres atomes de ces parois. Cette émission peut s’expliquer qualitativement de manière classique par des mouvements de particules chargées. Chaque atome, formé par le noyau de charge positive et le nuage électronique de charge négative qui gravite autour, se comporte comme un dipôle électrostatique, c’est-à-dire une charge positive associée à une charge négative. Sous l’effet de la température ce dipôle oscille aléatoirement et se comporte comme une antenne microscopique, excitée par un micro-courant, qui rayonne de l’énergie. Ce rayonnement à spectre continu occupe toute la cavité. Inversement le champ électrique met en mouvement ces charges et leur cède ainsi de l’énergie, ce qui constitue l’absorption. Un état d’équilibre est vite atteint de sorte que pendant une unité de temps l’énergie émise par les atomes est égale à l’énergie absorbée.
Ainsi la densité d’énergie électromagnétique ρ(T) (énergie par unité de volume de la cavité) est constante. Cette densité d’énergie provient de toutes les ondes de fréquence comprise entre 0 et l’infini. On observe que ρ(T) est proportionnelle à la puissance 4 de la température absolue T, soit ρ(T) = αT4. L’énergie totale, et donc le rayonnement émis, augmente considérablement avec la température. Ainsi le trou apparait très brillant lorsque la cavité est à haute température et totalement noir à très basse température.
Chaque contribution à la densité d’énergie à la fréquence ν, ρν(ν,T) , constitue ce qu’on appelle la densité énergétique spectrale. L’expérience montre qu’elle est la même en tout point de la cavité et qu’elle est indépendante de sa forme géométrique et de son volume ainsi que de la matière qui en constitue les parois : c’est une fonction universelle de ν et T. Pour mesurer cette fonction il suffit de percer un petit trou dans la cavité, et d’analyser le rayonnement qui en sort en fonction de ν et T.
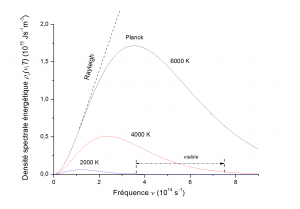
A chaque température on observe que la fonction ρν(ν,T) suit une courbe en cloche en fonction de la fréquence (Figure 2) présentant un maximum prononcé pour une valeur de la fréquence νm = 5,879 × 1010T (s-1) qui augmente linéairement avec la température exprimée en degrés K (kelvin). Ceci explique le changement de couleur d’un corps qui rayonne : le fer est rouge foncé à 680 °C (953 K), rouge clair à 810°C (1083 K), jaune à 1000 °C (1273 K) et blanc à 1200 °C (1473 K) [1].
3. Énergie rayonnée par un corps noir
La densité d’énergie à l’intérieur d’une cavité est une quantité difficile à mesurer directement, et on accède plutôt au flux d’énergie rayonnée par un petit trou de surface S. On peut mesurer ce flux en plaçant devant le trou un capteur dont le taux d’échauffement représentera l’énergie du rayonnement absorbé. Le flux d’énergie rayonné à travers une surface est défini comme l’énergie traversant cette surface par unité de temps et de surface. Si tout le rayonnement s’échappait perpendiculairement à la surface S à la vitesse c (Figure 3a), le contenu du volume Sc dt traverserait la surface en un temps dt. L’énergie correspondante serait donc ρSc dt. En divisant par le temps et la surface, on obtiendrait un flux d’énergie ρc directement lié à la densité d’énergie totale ρ.
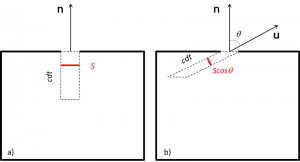
En réalité le flux sortant par la surface S est affecté d’un facteur ¼ dont l’origine est géométrique. En effet, à l’intérieur de la cavité le rayonnement se répartit dans toutes les directions de manière isotrope par réflexions multiples. Ainsi seule une petite partie du rayonnement sort au voisinage d’une direction représentée par le vecteur unitaire u faisant un angle θ avec la normale n (Figure 3b). Plus précisément dans un angle solide [2] très petit dΩ autour de u, seule la proportion dΩ/4π du rayonnement peut intervenir. De plus, comme dans le cas précédent, il faut considérer le contenu du cylindre oblique de la Figure 3b qui traverserait la surface en un temps dt. Ce cylindre a pour section normale à la direction de propagation S cosθ et pour longueur c dt. Ce volume est donc S cosθ cdt. Le flux élémentaire par unité de temps et de surface sortant est donc dΦ = ρ c cosθ dΩ/4π. La somme sur toutes les directions du rayonnement, c’est-à-dire sur le demi-espace à l’extérieur du trou, de cosθ dΩ/4π étant égale à ¼, on obtient un flux total d’énergie donné par la loi de Stefan-Boltzmann découverte empiriquement en 1871 :
Φ = ρ c/4 = σ T4 avec σ = 5,670×10-8 W.m-2.K-4
Les contributions à ce flux des rayonnements de fréquence ν sont égales à ρν(ν,T)c/4 et peuvent être mesurées. Notons bien que le rayonnement émis par le corps noir est tout à fait indépendant d’un rayonnement incident qui pénétrerait par le trou et serait totalement absorbé. Les fondements théoriques de ce rayonnement ont été posés dans le cadre de la thermodynamique par un étudiant en doctorat de Stefan, Ludwig Boltzmann en 1884, mais n’ont été élucidés que par Max Planck en 1901 grâce à la théorie des quanta (voir focus).
4. Émission et absorption, loi de Kirchhoff
Par définition, une surface est noire dans un certain domaine de fréquence si tout rayonnement électromagnétique dans ce domaine de fréquence est absorbé. Néanmoins cette surface réémet des ondes électromagnétiques par rayonnement thermique. Le flux Φ rayonné par une surface S à la température T est égal au flux émis par un petit trou de même surface dans une cavité à la même température. En effet, si l’on ferme le trou par la surface noire (Figure 3), à l’équilibre thermique, le flux issu de la surface noire vers l’intérieur de la cavité doit être égal mais opposé au flux thermique moyen issu de la cavité absorbé par la surface noire.
De même si un objet non noir à la température T absorbe une fraction a du rayonnement incident qui tombe sur lui, le flux de rayonnement émis par l’objet à la même température sera a fois le flux émis par un corps noir à cette température. Le facteur a désigne l’absorptivité. L’émissivité qui est le rapport entre l’émission de rayonnement d’une surface et celui d’un corps noir à la même température est désignée par le facteur e. La loi de Kirchhoff affirme que ces deux facteurs sont égaux, soit a = e. Pour un réflecteur parfait comme un miroir, a = 0, donc e = 0 : un réflecteur parfait ne rayonne pas thermiquement.
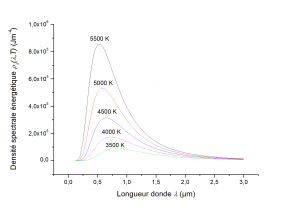
Souvent il est préférable d’exprimer la densité spectrale énergétique du corps noir en fonction de la longueur d’onde λ = c/ν plutôt que de la fréquence ν des ondes. Cette fonction ρλ(λ,T) s’obtient facilement à partir de ρν(ν,T) (voir focus). Le graphe de cette fonction, qui est représenté en fonction de λ pour diverses températures sur la Figure 4, a l’allure d’une courbe en cloche.

On montre sur la Figure 5 le rayonnement d’une lampe halogène qui correspond bien à celui d’un corps noir (e = 1) à 3450 K.
A température ordinaire les matériaux rayonnent dans l’infrarouge. Les émissivités des matériaux dépendent de la longueur d’onde mais aussi de l’état de leur surface. Typiquement [3] pour une feuille d’aluminium poli e (λ = 3 µm) = 0,09 et e (λ = 10 µm) = 0,04. Si l’on s’intéresse à l’émissivité totale e intégrée sur toutes les longueurs d’onde on a, par exemple, e = 0,02 pour l’or poli, e = 0,60 pour le sable, e = 0,80 pour la neige, e = 0,96 pour l’eau liquide, e = 0,70-0,90 pour le papier blanc, e = 0,90 pour le papier noir et e = 0,98 pour la peau humaine. Les sols et l’eau liquide ont des émissivités proches de 1, ce qui facilite la détermination des températures au sol par imagerie infrarouge de satellites.
5. Loi de Wien et applications à l’astrophysique
Les courbes ρλ(λ,T) représentées sur la Figure 4 présentent un maximum pour des valeurs λm données par la loi de Wien :
λmT = 0,201 hc/kB = 2,896×10-3 m.K
où h est la constante de Planck, c la vitesse de la lumière dans le vide et kB la constante de Boltzmann (lire Pression, température, chaleur). Cette expression très simple permet d’estimer des températures de surface.
–Température de la surface solaire
La surface solaire peut être considérée en première approximation comme une surface noire ; la densité ρλ(λ,T) du rayonnement solaire est maximale pour λm = 0,501 µm. A partir de la loi de Wien il est alors possible de déduire la température de la surface solaire TS = 5777 K.
–Flux de chaleur rayonné par le Soleil vers la Terre

–Température de rayonnement de la surface de la Terre
Ce sujet est traité dans l’article L’enveloppe gazeuse de la Terre.
–Rayonnement fossile de l’Univers
Penzias et Wilson ont découvert en 1964 l’existence d’un rayonnement fossile similaire à celui d’un corps noir avec un maximum à λm = 1,06 mm qui correspond à une température de 2,73 K. Ce rayonnement a une très faible anisotropie, c’est-à-dire qu’il varie très peu en fonction de l’orientation des antennes réceptrices. Cette observation apporte un soutien important au modèle du big-bang qui suppose un Univers en expansion qui se refroidit avec le temps. Selon cette théorie, le rayonnement cosmique subsiste depuis l’époque primaire où l’Univers était constitué d’électrons et de protons à environ 4000 K. Ce plasma d’électrons et de protons a fortement interagi avec le rayonnement électromagnétique à toutes les fréquences, de sorte que la matière et le rayonnement étaient en équilibre. L’Univers s’est ensuite refroidi vers 3000 K formant une matière essentiellement composée d’atomes d’hydrogène. L’interaction avec le rayonnement noir ne s’est plus effectuée qu’aux fréquences caractéristiques de l’hydrogène. La plus grande partie du rayonnement électromagnétique a donc été découplée de la matière et l’Univers s’est refroidi par détente adiabatique jusqu’à 2,73 K (de façon analogue à la détente d’un gaz). Après le découplage précédent, la matière a évolué en atomes plus lourds qui se sont organisés en galaxies, étoiles, nuages de poussière. Le rayonnement électromagnétique issu de ces objets se surajoute au rayonnement cosmique du corps noir.

6. Application aux caméras thermographiques
Une caméra thermographique [6] enregistre les différents rayonnements infrarouges qui varient en fonction de la température du corps qui émet. Elle permet ainsi de mesurer la température à partir de la loi du rayonnement du corps noir. Un filtre amovible permet d’intégrer le rayonnement dans des fenêtres spectrales de transparence de l’atmosphère. Le système convertit la puissance de rayonnement en signaux numériques ou analogiques : ceux-ci sont transcrits en température par le calculateur et transformés en image. L’image ainsi obtenue s’appelle « thermogramme ».

Une caméra thermique peut être utilisée dans de nombreuses situations : par les sapeurs pompiers pour la recherche de victimes de séismes et leur localisation dans des endroits difficilement accessibles ou pour la détection de feux naissant ou couvant, par les entreprises pour la détection des points faibles de l’isolation des bâtiments, dans les aéroports pour déceler les personnes ayant une fièvre suspecte, pour l’étude des espèces nocturnes telles les chauve-souris sans les déranger avec une source lumineuse visible.
Références et notes
Photo de couverture : Image thermique d’une bouche de métro anglais. [Source : branestawm2002 via Visual Hunt / CC BY]
[1] http://www.thethermograpiclibrary.org/index.php?title=Tableau_émissivités_en_thermographie
[2] De la même manière qu’un angle représente la longueur d’un arc de cercle de rayon unité, un angle solide représente une portion de surface sur une sphère de rayon unité. Pour un observateur situé en un point O, l’angle solide sous lequel on voit un objet est la projection de la surface apparente de cet objet sur une sphère de rayon unité centrée en O. Par exemple, à l’intérieur d’une cavité fermée, l’angle solide sous lequel on voit cette cavité n’est autre que la surface totale d’une sphère de rayon unité, c’est-à-dire 4π.
[3] http://www.thethermograpiclibrary.org/index.php?title=Tableau_émissivités_en_thermographie
[4] Elie Belorizky Initiation à la Mécanique quantique, Dunod, Paris, 2003.
[5] https://en.wikipedia.org/wiki/Cosmic microwave background
[6] A ne pas confondre avec les caméras dites infrarouges utilisées pour la simple vision nocturne, opérant à plus courte longueur d’onde (1 µm), ce qui ne permet pas des mesures thermiques.
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : BELORIZKY Elie, PIQUE Jean-Paul (20 septembre 2018), Le rayonnement thermique du corps noir, Encyclopédie de l’Environnement. Consulté le 27 juillet 2024 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/physique/le-rayonnement-thermique-du-corps-noir/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.







