Humid air and condensation

The first documented study of humid air seems to be the description made by Charles Leroy (1751), a physician from Montpellier (France). He explained in 1751 to the Royal Academy of Sciences that water can be dissolved in air as a function of air temperature, with the higher temperature corresponding to greater dissolution. To support his claim, he described several experiments. The most demonstrative one involves a bottle of air closed at daytime temperature. Once cooled at night, the air becomes unable to retain all the water dissolved at the higher temperature of the day: the excess water leads to the formation of condensed droplets that are clearly visible inside the bottle.

Indeed, air is never completely dry; it always contains, in an invisible way, water vapor whose concentration varies according to its temperature. In addition to steam, humid air can also contain water in a visible condensed state: liquid (fog droplets), solid (frosted fog). In these last cases, where vapor and condensed phases coexist, the humid air is said to be supersaturated.

We can therefore consider that humid air is formed of (1) dry air unlikely to condense under the temperature and pressure conditions considered here, and (2) water vapor likely to condense into liquid or ice. Dry air is composed primarily of nitrogen (≈ 78%) and oxygen (≈ 21%). For usual conditions of temperature and pressure encountered at the earth’s surface, both gases are far from their critical point coordinates and both fluids can be accepted as perfect gases. Air will therefore be considered as a single perfect gas. Water is also far from its critical point coordinates and can also be considered as a perfect gas.

1. Partial pressures: Dalton’s law

The partial pressure of a gas is the pressure that the gas would have if it were alone in a volume V. Dry air and water being both ideal gases, the total pressure is equal to the sum of the partial pressures: It is Dalton’s law. With p_a (resp p_v) the partial pressure of air (resp. water) and p_mthe total pressure, we obtain p_m = p_a + p_v. This rule of additivity corresponds to neglect the intermolecular forces between the gas molecules. The pressure being due to the impacts of the gas molecules in movement, the total pressure is simply the addition of the impacts of each type of molecules.

2. Equation of state

The equation of state for dry air and water vapor is the perfect gas equation p_iV=n_iRT where the subscript i represents air (i=a) or water vapor (i=v); n_i = m_i /M_i is the number of moles (i) of molar mass M_i and mass m_i in a volume V, R = 8.314 J.mole^-1.K^-1 is the molar constant of gases. The properties of moist air at a given partial pressure of water vapor can be deduced from this simple equation of state.

3. Saturation ; condensation

Consider the process of cooling at constant pressure p_m of a mass of moist air that contains a given mass of water. The conservation of mass requires that the total mass and the mass of water vapor remain constant during the process. The same applies to the number of moles of water vapor and the corresponding mole fraction n_v / n = p_v / p_m (from the perfect gas equation above and n =n_a+n_v). As a result, the pressure of the water vapor remains constant during the cooling process. In the atmosphere, the cooling of moist air therefore occurs at constant water vapor pressure.

During cooling, condensation to liquid can occur (see Clapeyron phase diagram in Figure 1). Consider a mass of moist air initially at point A on the T₁ isotherm. When the temperature decreases at constant pressure pv(T₁), its volume also decreases. The liquid-vapor coexistence curve (the saturation curve) is reached (point B) at a certain temperature T₂ and drops of liquid may appear. Point B is called the dew point and T₂ is the dew point temperature T_d. The vapor pressure is the saturation pressure at temperature T_d, p_s(T_d) = p_v(T₁) where condensation of water vapor can begin. When the air is cooled further, condensation continues at constant pressure pv and temperature T_d. The cooling energy only compensates for the release of the latent heat of condensation (Read: Pressure, Temperature and Heat). In C, all the water contained in the humid air has condensed. The BC zone is the fog zone where liquid droplets coexist with the vapor. Further cooling (to point D) involves only the liquid.

The liquid-vapor saturation curve represents in the pv -T plane the liquid-vapor equilibrium (Figure 2). At a given temperature, the maximum pressure above which water vapor turns into liquid water is the saturated vapor pressure p_s. Therefore, in a given mass of moist air, the vapor pressure can be such that (i) p_v <p_{s :} the water in the moist air is in the vapor state; (ii) p_v = p_s: the water in the moist air is both in the vapor and liquid state because the phase change occurs at constant pressure p_s= p_v(T_d) = p_v(T₁).

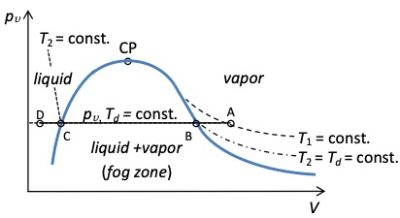
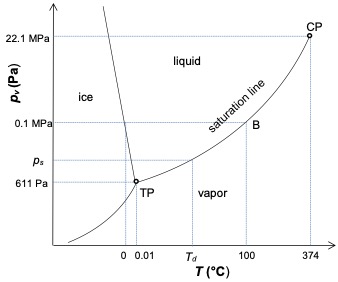
Moist air can be saturated (point B in Figure 1) or supersaturated, when liquid droplets (mist) are present (line BC in Figure 1).

Saturated vapor pressure can then be achieved in a given moist air in two ways. (i) By cooling a given mass of moist air: the vapor pressure remains constant at pv but p_s decreases until equality p_v= p_s(T_d) is satisfied. (ii) Adding a mass of water to a given volume of humid air at constant temperature: the vapour pressure increases until it reaches p_v=p_s at the same temperature. If we add more water at constant temperature, we obtain the coexistence of the saturated vapor pressure and the liquid. The humid air is then supersaturated.

From the above, we can define the relative humidity RH as the ratio, at a given temperature, between the vapor pressure and the saturated vapor pressure, RH = p_v(T)/p_s(T). When a given mass of moist air is cooled, RH increases to 100% at the saturation line. When water is added at constant temperature, RH also increases to 100% and reaches the saturation line. Relative humidity is a common index for determining how close a given humid air is to saturation. The higher the RH, the less cooling or mass addition required to achieve condensation.

Notes

Cover image. [Source: royalty free]