L’émission, la propagation et la perception du son
PDF
Douces notes de musique, ronronnement d’un moteur, stridences d’un marteau-piqueur… Comment les sons sont-ils produits et comment parviennent-ils jusqu’à nos oreilles ? Le son est composé d’oscillations qui se propagent dans les milieux compressibles notamment dans les fluides et les solides, avec des caractéristiques qui sont propres à chacun d’eux. Dans cet article, les notions de fréquence, de longueur d’onde et de puissance sonore sont dévoilées. Nous irons même un peu plus loin en dégageant les concepts de modes propres et de résonance, illustrés par les exemples de la balançoire et de la musique produite par un violon.
1. Le son, qu’est-ce que c’est ?

Le fluide ambiant transmet sa propre vibration à son voisinage, en forçant les couches de molécules les plus proches à suivre ses allers et retours. A leur tour, elles transmettent aux couches voisines ces alternances de compressions et de détentes, et ainsi de suite (voir l’animation de l’image de couverture). L’air apparemment au repos, mais dont nous savons bien qu’il est constitué de molécules en perpétuelle agitation et qu’il est compressible [1], est très sensible à ces secousses qui, alternativement, resserrent puis écartent les couches de molécules. L’eau, beaucoup plus dense que l’air (environ 800 fois) et beaucoup moins compressible (environ 100 000 fois), est aussi constituée de molécules en agitation, mais celles-ci se repoussent avec des forces coulombiennes [2] très difficiles à vaincre. Comme l’eau, les liquides sont donc aussi capables de véhiculer des sons.
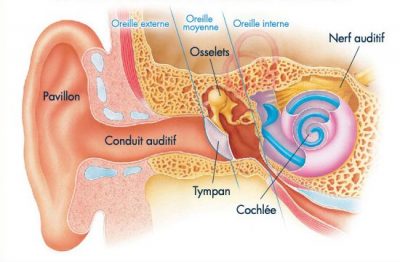
2. Célérité, fréquence et longueur d’onde
Dans un gaz comme l’air la propagation du son résulte d’une propriété essentielle : la mobilité des molécules, avec une vitesse moyenne de l’ordre de 480 m/s dans les conditions normales (lire l’article Pression, température, chaleur). Mais cette agitation n’a pas d’orientation privilégiée : elle diffuse l’énergie de la secousse dans toutes les directions. Or la vitesse de propagation du son dans l’air, que l’on appelle célérité, implique que toutes les molécules situées dans un très petit volume (la particule fluide) subissent un même déplacement ordonné et collectif. Ceci explique que la célérité du son, bien que liée à la vitesse moyenne des molécules, ne soit qu’une fraction de cette vitesse moyenne, de l’ordre de 340 m/s.
Cette célérité du son est très faible par rapport à la vitesse de la lumière (300 000 km/s dans le vide et presque autant dans l’air). Ceci explique que le spectateur d’un match de football, assis dans les tribunes à une distance d’environ 170 m du rond central, n’entende la frappe du joueur qu’une demi-seconde après avoir vu son pied frapper le ballon. A l’inverse, sur des distances assez courtes comme les dimensions d’une salle de concert, les ondes sonores sont capables de véhiculer avec fidélité des informations d’une très grande subtilité, que les mélomanes apprécient. Petit exercice bien connu : par temps d’orage, sachant que la perception de l’éclair est quasi-instantanée, comment peut-on évaluer à quelle distance l’orage vient d’éclater ?

Dans notre environnement, tout bouge sans cesse et émet donc des sons. Dans nos propres corps, le sang circule, les poumons se gonflent et se dégonflent, le système digestif lui aussi est animé. Mais nos chairs relativement molles amortissent bien ces variations de pression ; ceci impose au médecin l’utilisation d’un stéthoscope pour entendre les battements de nos cœurs ou les fluctuations de vitesse de l’air dans nos bronches. Par ailleurs, les oreilles humaines ne sont sensibles qu’à une bande de fréquences assez étroite, entre 15 Hz et 15 000 Hz. C’est pour cela que nous ne percevons pas nos bruits intérieurs, à l’exception de notre propre voix. Ceci nous permet de fixer notre attention sur les bruits venant de l’extérieur, souvent plus agréables, et surtout plus utiles par toutes les informations qu’ils nous permettent de capter. D’autres espèces animales perçoivent des sons dans des bandes de fréquences très différentes. Les éléphants émettent et entendent des infrasons de fréquence inférieure à 10 Hz, qu’ils utilisent pour communiquer entre eux. A l’autre extrémité, les chauves-souris émettent et entendent des ultrasons de fréquence supérieure à 30 000 Hz, dont les échos réverbérés par leur environnement leur permettent d’en prendre connaissance dans l’obscurité la plus totale.
D’une manière générale la célérité du son est pratiquement indépendante de la fréquence. Cependant elle dépend de la masse volumique du milieu et, par là, elle est est assez sensible aux variations de température et de pression. Cette célérité est d’autant plus grande que la masse volumique du milieu et sa compressibilité sont plus petits. Ainsi, dans l’hélium, dont la compressibilité est voisine de celle de l’air mais dont la densité est beaucoup plus faible, la célérité du son est presque 3 fois plus grande que dans l’air.
3. La puissance sonore
Pour caractériser la puissance d’un son, il est courant d’utiliser la pression acoustique p, amplitude maximale de la fluctuation locale de la pression atmosphérique. D’ordinaire, cette fluctuation est très faible. A titre d’exemple, une personne parlant normalement produit une pression acoustique de l’ordre de 0,01 pascal (Pa) à un mètre de distance, soit 10 millions de fois moins que la pression atmosphérique normale, voisine de 100000 Pa.
Cette pression acoustique est proportionnelle à l’amplitude maximale des vibrations montrées sur la figure 2. En réalité, la sensation perçue par l’oreille humaine est plutôt proportionnelle au logarithme [3] de la pression qu’à la pression elle-même. Ceci signifie qu’une pression acoustique 10 fois plus forte est ressentie comme un son 2 fois plus intense, une pression acoustique 100 fois plus forte comme un son 4 fois plus intense. La puissance transportée par une onde sonore étant proportionnelle au carré de la pression acoustique, ceci a conduit à caractériser la puissance d’un son par la quantité 10 log10 (p2/p2réf)=20 log10(p/préf), nommée le décibelLe décibel (dB), ou dixième du Bel, est l’unité de puissance sonore couramment utilisée, ainsi nommée en hommage à Graham Bell (1847-1922), scientifique écossais inventeur du téléphone. Il est égal à 20 log10(p/préf) où p désigne la pression acoustique et préf une pression de référence fixée arbitrairement à 20 μPa (20×10-6 Pascal, soit 0,2 milliardième de la pression atmosphérique), ce qui représente le seuil d’audition chez la plupart des humains.{end-tooltip} [4] et notée dB, où préf est une pression de référence fixée arbitrairement à 20 μPa (20 × 10-6 Pascal, soit 0,2 milliardième de la pression atmosphérique). Cette référence correspond au seuil d’audibilité chez la plupart des gens c’est à dire à 0 dB. Ainsi, un accroissement de 20 du nombre de décibels représente une multiplication par 10 de l’amplitude de la pression acoustique, soit encore une multiplication par 100 de la puissance sonore, encore appelée l’intensité du son. Voici quelques ordres de grandeur qui donnent une signification pratique au décibel :
- Atmosphère campagnarde calme : 40 dB ou p=2 × 10-8 fois la pression atmosphérique.
- Rue animée avec circulation automobile : 80 dB ou p=2 × 10-6 fois la pression atmosphérique.
- Aéroport avec avion au décollage : 120 dB ou p=2 × 10-4 fois la pression atmosphérique.
- Limite légale de sécurité pour une exposition brève : 135 dB ou un millième de la pression atmosphérique.
Chacun sait qu’il est nécessaire d’élever de plus en plus la voix pour appeler une personne qui s’éloigne. En se propageant, le son émis par une source quelconque perd en effet assez rapidement son intensité, pour deux raisons. Tout d’abord, puisque son énergie se répartit sur un front hémisphérique de plus en plus vaste au fur et à mesure que le front d’onde s’éloigne du lieu d’émission, son intensité diminue en raison inverse de l’aire de ce front, c’est à dire comme l’inverse du carré de la distance à la source. Par ailleurs, cette énergie initiale, faite de compressions et de détentes du gaz, est progressivement dissipée en chaleur par la viscosité (lire l’article Pression, température et chaleur).
4. Oscillations simples : le pendule et la balançoire

Supposons maintenant que l’on apporte au pendule une énergie supplémentaire en choisissant bien la fréquence de cet apport. Exemple : à chaque passage du pendule par son point bas, on le pousse pour lui fournir une vitesse supplémentaire ; cette énergie va s’ajouter à l’énergie antérieure du pendule et l’amplitude de ses oscillations va s’accroître. On dit alors que la fréquence de cette nouvelle excitation est en phase avec l’oscillation du pendule et qu’elle conduit à une résonance du pendule. Cette résonance se traduit par de grandes amplitudes, telles que, à chaque oscillation, l’apport d’énergie soit exactement égal à l’énergie dissipée.

Le cas de la balançoire (Figure 5) montre une autre forme de résonance. Avec un peu d’entraînement, les enfants parviennent à s’élancer lors du passage au point bas et à accroître ainsi l’amplitude de l’oscillation. On remarquera d’ailleurs qu’ils apportent une énergie supplémentaire tout en réduisant la résistance de l’air en s’allongeant le mieux possible le long de leur trajectoire quand la balançoire passe à son point bas.
5. Ondes stationnaires : corde vibrante et musique
Ni le pendule ni la balançoire ne produisent des sons (seuls les grincements de leurs fixations peuvent être audibles). Au-delà de ce cas simple, une nouvelle étape doit être franchie pour illustrer comment un corps oscillant produit des sons. Le prototype d’un tel système est la corde tendue entre deux points fixes, soumise à une excitation, qui vibre et émet des sons. C’est le procédé utilisé pour produire de la musique avec les violons, les guitares, les harpes et autres instruments à corde. Ces systèmes mécaniques sont fort complexes, car ils possèdent une infinité de degrés de liberté – toutes les positions possibles – et autant de modes propres. Parmi ceux-ci, on distingue le mode fondamental, tel qu’une seule demi-longueur d’onde soit présente entre les deux points fixes, et ses harmoniques dont les fréquences sont des multiples de la fréquence fondamentale. L’animation de la Figure 6 illustre les trois premiers modes, l’imagination permet de deviner la suite infinie des harmoniques non représentée.
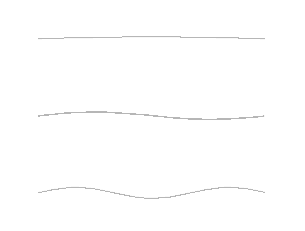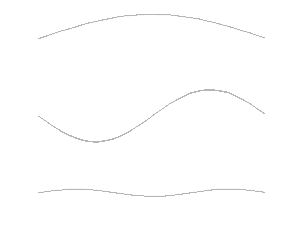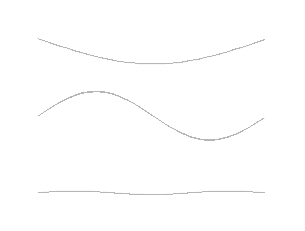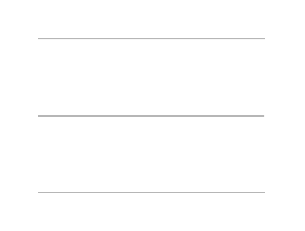
Il est aussi possible de créer des ondes stationnaires entre un point fixe et une extrémité libre. Le mode fondamental comprend alors seulement un quart de longueur d’onde entre ces deux extrémités. Même s’il est formé de deux branches métalliques au lieu d’une corde vibrante, le diapason illustre fort bien ce système, à tel point que son aptitude à émettre un « la » d’une pureté assez grande peut devenir la référence pour un orchestre entier.
L’oscillation de la corde vibrante est audible mais non visible. En revanche, celle du tube de feu de la Vidéo ci-dessous montre qu’il est possible de visualiser les fluctuations périodiques de la pression au sein du gaz propane présent dans cet appareil. Le débit du gaz à travers les orifices distribués le long du tube et la hauteur de chaque petite flamme sont proportionnels à cette pression : nuls aux nœuds et maximaux aux ventres.
Video. Le tube de feu de Ruben. Un haut parleur envoie des ondes acoustiques dans un long tube où des ondes stationnaires s’installent pour une gamme de fréquences qui entrent en résonance avec ce tube. A l’extrémité gauche du propane est pompé dans le tube ; il en ressort par une série d’orifices situés sur la génératrice supérieure, créant ainsi une flamme longitudinale. La hauteur locale de cette flamme, proportionnelle à la pression locale dans le tube met en évidence les ventres et les nœuds au sein de celui-ci.
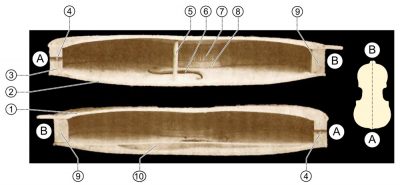
[Source : By English: Unknown photograph. Improved and (a little) colorised by Dake. Numbering added by SuperManu / Français : Le photographe original est inconnu. La photo a été nettoyée et un peu colorée par Dake. Les chiffres ont été ajoutés par SuperManu. (L’Art du luthier (Auguste Tolbecque)) [GFDL (http://www.gnu.org/copyleft/fdl.html), CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/), CC BY-SA 2.5-2.0-1.0 (http://creativecommons.org/licenses/by-sa/2.5-2.0-1.0), GFDL (http://www.gnu.org/copyleft/fdl.html), CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/) or CC BY-SA 2.5-2.0-1.0 (http://creativecommons.org/licenses/by-sa/2.5-2.0-1.0)], via Wikimedia Commons]
Falaises rocheuses, enceinte d’un théâtre antique, mur anti-bruit… Chacun sait que des parois, naturelles ou artificielles, peuvent avoir une influence sur le signal perçu par l’auditeur. Cette influence tient à la fois à leur forme, plus ou moins favorable à des résonances, et à leur état de surface. Des parois lisses, fermes et élastiques réverbèrent bien le son ; à l’inverse, les parois rugueuses, ou revêtues avec des matériaux souples et absorbants, le réverbèrent mal. On touche ici au phénomène de l’écho, dont l’analyse débouche sur des applications importantes comme la conception de salles de concert de haute qualité acoustique, ou la protection contre les nuisances sonores.
6. Propagation du son dans l’eau et dans les solides
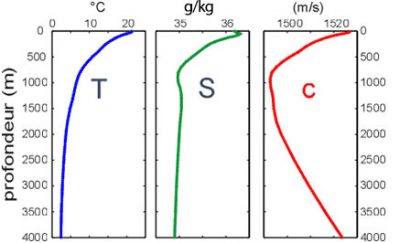
Puisqu’il résulte de leur compressibilité, le son se propage dans tous les milieux, notamment dans les liquides comme l’eau. Dans les mers ce phénomène présente un intérêt considérable, puisque, la lumière ne pénétrant pas dans les grandes profondeurs, il fournit l’un des moyens de diagnostic privilégiés. C’est avec des sons ou des ultrasons que les pêcheurs détectent les bancs de poissons, que les géographes relèvent les reliefs sous-marins et que les marines nationales du monde entier repèrent les navires et les submersibles amis ou ennemis présents dans leur voisinage. C’est aussi avec des ultrasons que les mammifères marins communiquent. La gamme des fréquences utilisables dans l’eau de mer s’étend de 30 Hz à 1,5 MHz, une valeur 100 fois plus élevée que la limite audible pour l’homme, voisine de 15 000 Hz. La célérité du son dans l’eau est voisine de 1450 à 1550 m s-1. Comme le montre la Figure 8, elle varie surtout avec la température et la profondeur, c’est à dire avec la pression, mais elle est peu sensible aux variations de salinité (lire l’article Le milieu marin).
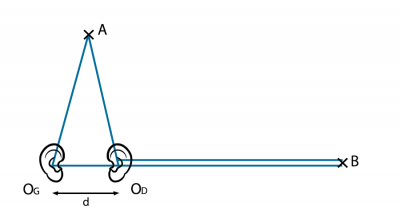
Le corps humain, en grande partie composé d’eau, ne réfléchit pas les ondes acoustiques sous marines. En raison de la distance entre leurs oreilles (d, environ 17 cm), les humains perçoivent dans l’air deux sons dont le déphasage permet de déceler la provenance. Nous avons vu que pour un son de fréquence égale à 1000 Hz, la longueur d’onde est égale à 34 cm. Si l’émetteur est situé devant cet humain (point A sur la Figure 9), à égale distance des deux oreilles, celles-ci perçoivent ce son en même temps, sans aucun déphasage. Mais si l’émetteur est situé dans la ligne des oreilles (point B sur la Figure 9), les sons perçus par celles-ci ont un décalage temporel d/c de 1/2000 s et une valeur d/λ de 17/34, soit une demi longueur d’onde [7]. Ce déphasage significatif permet au cerveau de ressentir un relief sonore, c’est à dire de savoir d’où provient le son. C’est ce déphasage qui permet au chef d’orchestre de déceler le son émis par chaque instrument au sein d’un ensemble musical.
Au contraire, dans l’eau, le décalage temporel entre les sons perçus par les deux oreilles (d/c) est de l’ordre de 1/10 000 s (lorsque l’émetteur est situé sur le côté), et leur déphasage maximal. La valeur de d se réduit alors au dixième de la longueur d’onde pour une fréquence de 1000 Hz et devient trop faible pour permettre cette détection. Immergés dans l’eau, les humains sont donc incapables de ressentir le relief sonore. En revanche, les mammifères marins comme les dauphins émettent des sons de fréquences 10 à 100 fois plus élevées que la plus haute fréquence perçue par l’oreille humaine. Leur longueur d’onde (λ), située entre 1,5 et 15 cm, est alors inférieure à la distance entre leurs oreilles (environ 15 cm). Le déphasage entre ces sons se réduit alors à une fraction significative de la longueur d’onde même lorsque l’émetteur n’est pas dans la ligne de leurs oreilles. Il leur permet, non seulement de communiquer entre eux, mais aussi de se situer les uns par rapport aux autres et par rapport à tout obstacle éventuel dans l’obscurité des fonds marins.
Dans les milieux solides, le son se propage encore plus rapidement que dans les liquides. Ceci tient au fait que les solides sont encore moins compressibles que les liquides. Ainsi, dans l’acier de l’enclume évoquée au début de cet article, la célérité est de l’ordre de 5000 m/s. Si sa longueur est voisine de 50 cm, cela signifie que l’enclume toute entière a ressenti le choc du marteau en un dix millième de seconde, alors que les ondes sonores dans l’air voisin mettent presque 2 millisecondes pour parcourir la même distance. Autrement dit, approximativement, c’est l’enclume toute entière, et pas seulement la zone impactée par le marteau, qui émet en bloc le son entendu par le forgeron.
Références et notes
Image de couverture : Les ondes acoustiques émises par une sphère vibrante radialement, se propagent dans toutes les directions sous forme d’alternances de compressions et de détentes des couches gazeuses voisines les unes des autres. [Source : By Thierry Dugnolle (Own work) [CC0], via Wikimedia Commons]
[1] La compressibilité de l’air est à la fois assez grande pour que ce milieu fluide puisse transporter le son et assez faible pour justifier l’usage d’approximations incompressibles pour décrire l’aérodynamique à des vitesses nettement inférieures à la célérité du son.
[2] Les charges électriques négatives des électrons qui entourent les noyaux des atomes d’hydrogène et d’oxygène formant la molécule d’eau sont soumises à la force de Coulomb qui les repousse fortement les uns des autres lorsque leur distance devient très petite. A leur tour, ces électrons transmettent cette force de répulsion aux atomes et aux molécules.
[3] Le logarithme est l’opération mathématique qui permet de substituer une addition à une multiplication : log (ab) =log(a)+log(b). Multiplier la pression acoustique par 10, nombre dont le logarithme décimal est l’unité, se traduit alors par l’ajout d’une unité à son logarithme. Dans les notations usuelles, log10 désigne le logarithme décimal, tandis que Log désigne le logarithme népérien, dont la base est le nombre irrationnel e = 2,71828…
[4] Dénomination en hommage à Graham Bell (1847-1922), scientifique écossais inventeur du téléphone. Le décibel (dB) est le dixième du Bel, très rarement utilisé.
[5] La tessiture d’un son caractérise sa hauteur, c’est-à-dire sa fréquence, qu’il s’agisse d’un son produit par un instrument ou d’une voix humaine. La tessiture du violon se situe entre 300 et 1400 Hz, celle du violoncelle entre 70 et 750 Hz et celle de la contrebasse entre 60 et 350 Hz.
[6] Un guide d’ondes est un système physique qui sert à confiner les ondes dans un milieu particulier, au moins sur une certaine distance. Il est très utilisé avec la lumière et les ondes électromagnétiques en général, par exemple dans les fibres optiques. Dans le cas des ondes acoustiques, notamment dans l’eau de mer, son efficacité est moins nette en raison de la nature plus floue des interfaces qui ne canalisent pas de la même façon les différentes longueurs d’ondes.
[7] A une différence d’orientation de 90 degrés des émetteurs A et B sur la Figure 9, on peut donc associer un déphasage 360/20 = 18 degrés par rapport à l’axe du corps de cet humain, ceci pour une fréquence de 100 Hz pour laquelle d/λ=1/20. Le rapport 18/90 = 1/5 caractérise la sensibilité des humains au relief sonore dans l’air.
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : MOREAU René (27 juin 2018), L’émission, la propagation et la perception du son, Encyclopédie de l’Environnement. Consulté le 27 juillet 2024 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/physique/lemission-propagation-perception/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.







