The emission, propagation and perception of sound
PDF
Soft notes of music, the hum of an engine, the stridence of a jackhammer… How are sounds produced and how do they get to our ears? Sound is composed of oscillations that propagate in compressible media, especially in fluids and solids, with characteristics that are specific to each of them. In this article, the concepts of frequency, wavelength and sound power are discussed. We will even go a little further by identifying the concepts of proper modes and resonance, illustrated by the examples of the swing and the music produced by a violin.
1. What is sound? What is it?

The ambient fluid transmits its own vibration to its surroundings, forcing the nearest layers of molecules to follow its movements back and forth. In turn, they transmit to the adjacent layers these alternating compression and relaxation, and so on (see the animation of the cover image). The air, apparently at rest, but which we know well that it consists of molecules in perpetual agitation and that it is compressible [1], is very sensitive to these tremors which, in turn, tighten and then remove the layers of molecules. Water, much denser than air (about 800 times) and much less compressible (about 100,000 times), is also made up of molecules in agitation, but these repel each other with Coulomb forces [2] that are very difficult to overcome. Like water, liquids are therefore also capable of carrying sounds.
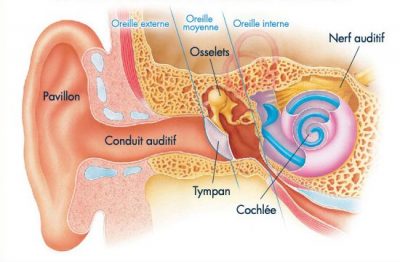
2. Speed, frequency and wavelength
In a gas like air, sound propagation results from an essential property: the mobility of molecules, with an average speed of about 480 m/s under normal conditions (see the article Pressure, temperature, heat). But this agitation does not have a privileged orientation: it diffuses the energy of the tremor in all directions. However, the speed of sound propagation in the air, called celerity, implies that all molecules located in a very small volume (the fluid particle) undergo the same ordered and collective displacement. This explains why the speed of sound, although linked to the average speed of molecules, is only a fraction of this average speed, around 340 m/s.
This sound velocity is very low compared to the speed of light (300,000 km/s in vacuum and almost as much in air). This explains why the spectator of a football match, sitting in the stands at a distance of about 170 m from the centre circle, only hears the player’s shot half a second after seeing his foot hit the ball. On the other hand, over relatively short distances such as the dimensions of a concert hall, sound waves are able to accurately convey very subtle information that music lovers appreciate. A well-known exercise: in stormy weather, knowing that the perception of lightning is almost instantaneous, how can we assess how far away the storm has just broken?

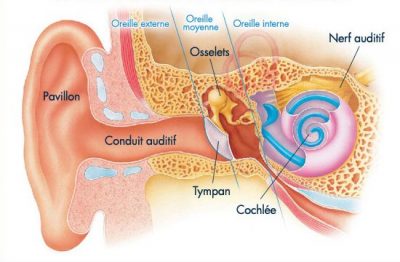
In our environment, everything is constantly moving and therefore emitting sounds. In our own bodies, blood circulates, the lungs swell and deflate, the digestive system is also animated. But our relatively soft flesh absorbs these pressure variations well; this requires the doctor to use a stethoscope to hear the beats of our hearts or the fluctuations in air velocity in our bronchi. In addition, human ears are only sensitive to a relatively narrow frequency band, between 15 Hz and 15 000 Hz. That is why we do not perceive our inner noises, except for our own voice. This allows us to focus our attention on the noises coming from the outside, often more pleasant, and above all more useful by all the information they allow us to capture. Other animal species perceive sounds in very different frequency bands. Elephants emit and hear infrasound frequencies of less than 10 Hz, which they use to communicate with each other. At the other end, bats emit and hear ultrasounds with a frequency greater than 30,000 Hz, whose echoes reflected by their environment allow them to read them in complete darkness.
Generally speaking, the speed of sound is practically independent of frequency. However, it depends on the density of the medium and is therefore quite sensitive to temperature and pressure variations. This speed is all the greater as the density of the medium and its compressibility are smaller. Thus, in helium, whose compressibility is close to that of air but whose density is much lower, the speed of sound is almost 3 times greater than in air.
3. The sound power
To characterize the power of a sound, it is common to use the sound pressure p, the maximum amplitude of the local fluctuation of atmospheric pressure. Usually, this fluctuation is very small. For example, a normally speaking person produces an acoustic pressure of about 0.01 pascal (Pa) at a distance of one metre, 10 million times less than the normal atmospheric pressure, close to 100000 Pa.
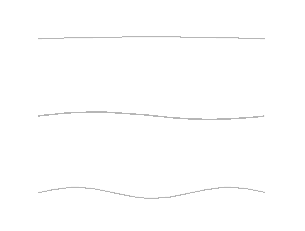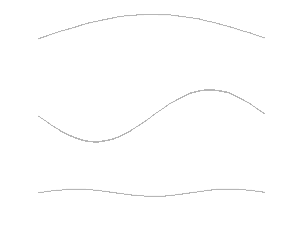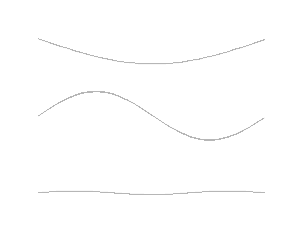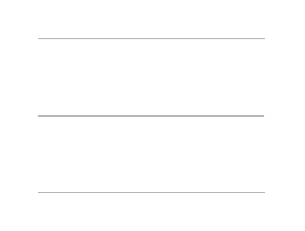
This sound pressure is proportional to the maximum amplitude of the vibrations shown in Figure 2; in reality, the sensation perceived by the human ear is more proportional to the logarithm [3] of the pressure than to the pressure itself. This means that a sound pressure 10 times higher is felt as a sound twice as intense, a sound pressure 100 times higher as a sound 4 times more intense. The power carried by a sound wave being proportional to the square of the sound pressure, this led to characterize the power of a sound by the quantity 10 log10 (p2/p2ref)=20 log10 (p/pref), named the decibel. The decibel (dB), or tenth of the Bel, is the commonly used sound power unit, so named in tribute to Graham Bell (1847-1922), a Scottish scientist who invented the telephone. It is equal to 20 log10 (p/pref) where p denotes the acoustic pressure and pref a reference pressure arbitrarily set at 20 μPa (20×10-6 Pascal, or 0.2 billionth of atmospheric pressure), which represents the hearing threshold in most humans. [4] and noted dB, where pref a reference pressure arbitrarily set at 20 μPa (20 × 10-6 Pascal, or 0.2 billionth of atmospheric pressure). This reference corresponds to the audibility threshold for most people, i.e. 0 dB. Thus, a 20-decibel increase in the number of decibels represents a 10-fold increase in the amplitude of sound pressure, or a 100-fold increase in sound power, also called sound intensity.
Here are some orders of magnitude that give practical meaning to the decibel:
- Quiet country atmosphere: 40 dB or p=2 × 10-8 times atmospheric pressure.
- Bustling street with traffic: 80 dB or p=2 × 10-6 times atmospheric pressure.
- Airport with aircraft at take-off: 120 dB or p=2 × 10-4 times atmospheric pressure.
- Legal safety limit for short exposure: 135 dB or one thousandth of atmospheric pressure.
Everyone knows that it is necessary to raise your voice more and more to call someone who is moving away. As it propagates, the sound emitted by any source loses its intensity quite quickly, for two reasons. First, since its energy is distributed over an increasingly large hemispheric front as the wavefront moves away from the emission site, its intensity decreases due to the opposite of the area of this front, i.e. as the inverse of the square of the distance to the source. In addition, this initial energy, made up of gas compression and expansion, is gradually dissipated into heat by viscosity (see the article Pressure, Temperature and Heat).
4. Simple oscillations: the pendulum and the swing

Now suppose that we bring additional energy to the pendulum by choosing the frequency of this input carefully. Example: each time the pendulum passes through its low point, it is pushed to provide it with an additional speed; this energy will be added to the previous energy of the pendulum and the amplitude of its oscillations will increase. It is then said that the frequency of this new excitation is in phase with the oscillation of the pendulum and that it leads to a resonance of the pendulum. This resonance results in large amplitudes, such that, at each oscillation, the energy supply is exactly equal to the energy dissipated.

The case of the swing (Figure 5) shows another form of resonance. With a little practice, the children can launch themselves into the low point and thus increase the amplitude of the oscillation. It should also be noted that they provide additional energy while reducing the resistance of the air by lying as far as possible along their trajectory when the swing passes at its low point.
5. Stationary waves: vibrating string and music
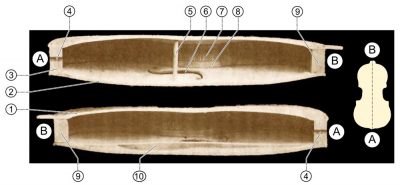
Neither the pendulum nor the swing produce sounds (only the squeaks of their fasteners can be heard). Beyond this simple case, a new step must be taken to illustrate how an oscillating body produces sounds. The prototype of such a system is the rope stretched between two fixed points, subjected to excitation, which vibrates and emits sounds. This is the process used to produce music with violins, guitars, harps and other stringed instruments. These mechanical systems are very complex, because they have an infinite number of degrees of freedom – all possible positions – and as many different modes. Among these, we distinguish the fundamental mode, such that only one half wavelength is present between the two fixed points, and its harmonics whose frequencies are multiples of the fundamental frequency. The animation in Figure 6 illustrates the first three modes, the imagination makes it possible to guess the infinite sequence of harmonics not represented.
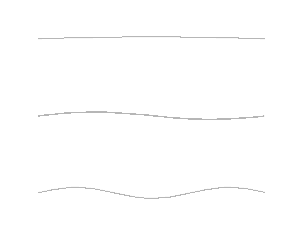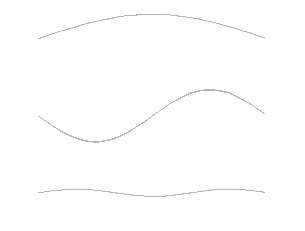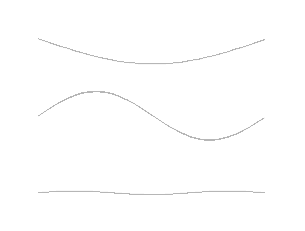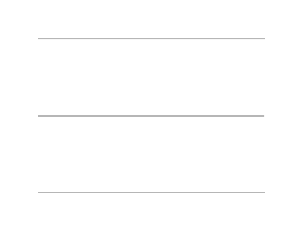
It is also possible to create standing waves between a fixed point and a free end. The fundamental mode then includes only a quarter wavelength between these two ends. Although it consists of two metal branches instead of a vibrating string, the tuning fork illustrates this system very well, to such an extent that its ability to emit an “A” of quite high purity can become the reference for an entire orchestra.
The oscillation of the vibrating string is audible but not visible. On the other hand, the one in the fire tube of the Video below shows that it is possible to visualize the periodic fluctuations in pressure within the propane gas present in this appliance. The flow of gas through the orifices distributed along the tube and the height of each small flame are proportional to this pressure: zero at knots and maximum at bellies.
Video. Ruben’s fire tube. A loudspeaker sends acoustic waves into a long tube where standing waves are installed for a range of frequencies that resonate with the tube. At the left end of the propane is pumped into the tube; it exits through a series of holes on the upper generator, creating a longitudinal flame. The local height of this flame, proportional to the local pressure in the tube, highlights the bellies and knots within it.
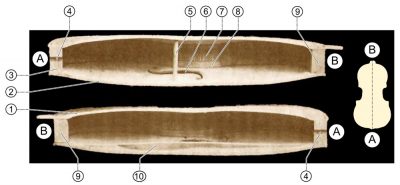
Source: By English: Unknown photograph. Improved and (a little) colorised by Dake. Numbering added by SuperManu / French: The original photographer is unknown. The photo was cleaned and a little bit colored by Dake. The figures have been added by SuperManu. (L’Art du luthier (Auguste Tolbecque))[Source : GFDL (http://www.gnu.org/copyleft/fdl.html), CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/), CC BY-SA 2.5-2.0-1.0 (http://creativecommons.org/licenses/by-sa/2.5-2.0-1.0), GFDL (http://www.gnu.org/copyleft/fdl.html), CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/) or CC BY-SA 2.5-2.0-1.0 (http://creativecommons.org/licenses/by-sa/2.5-2.0-1.0)], via Wikimedia Commons]
Rocky cliffs, an ancient theatre enclosure, a noise barrier… Everyone knows that natural or artificial walls can have an influence on the signal perceived by the listener. This influence is due both to their shape, more or less favourable to resonances, and to their surface condition. Smooth, firm and elastic walls reflect sound well; on the other hand, rough walls, or walls coated with soft and absorbent materials, do not reflect it well. This concerns the phenomenon of echo, the analysis of which leads to important applications such as the design of concert halls of high acoustic quality, or protection against noise pollution.
6. Sound propagation in water and solids
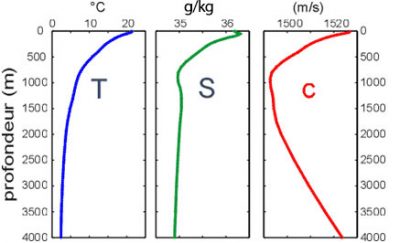
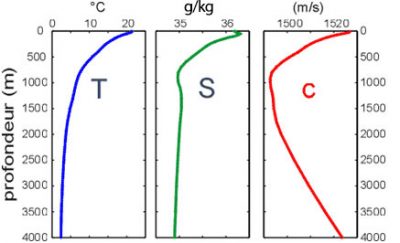
Because it results from their compressibility, sound spreads in all media, especially in liquids such as water. In the seas, this phenomenon is of considerable interest because, since light does not penetrate to great depths, it provides one of the preferred means of diagnosis. Fishermen use sound or ultrasound to detect schools of fish, geographers survey underwater landforms and national navies around the world identify ships and submersible friends or enemies in their vicinity. It is also with ultrasound that marine mammals communicate. The range of frequencies that can be used in seawater ranges from 30 Hz to 1.5 MHz, a value 100 times higher than the human audible limit of about 15,000 Hz. The speed of sound in the water is about 1450 to 1550 m s-1. As shown in Figure 8, it varies mainly with temperature and depth, i.e. with pressure, but is not very sensitive to changes in salinity (see the article The Marine Environment).
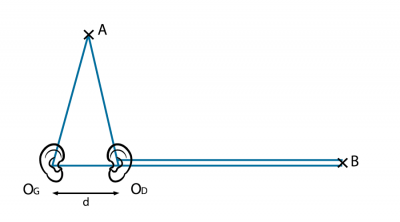
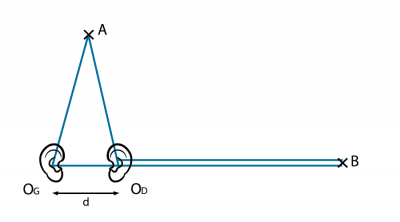
The human body, largely composed of water, does not reflect underwater sound waves. Because of the distance between their ears (about 17 cm), humans perceive two sounds in the air whose phase shift makes it possible to detect their origin. We have seen that for a sound with a frequency equal to 1000 Hz, the wavelength is equal to 34 cm. If the transmitter is located in front of this human (point A in Figure 9), at equal distance from both ears, they perceive this sound at the same time, without any phase shift. But if the transmitter is located in the ear line (point B in Figure 9), the sounds perceived by the ears have a time shift d/c of 1/2000 s and a value d/λ of 17/34, or half a wavelength [7]. This significant phase shift allows the brain to feel a sound relief, i.e. to know where the sound comes from. It is this phase shift that allows the conductor to detect the sound emitted by each instrument within a musical ensemble.
On the contrary, in water, the time difference between the sounds perceived by the two ears (d/c) is about 1/10,000 s (when the transmitter is located on the side), and their maximum phase shift. The value of d is then reduced to one-tenth of the wavelength at a frequency of 1000 Hz and becomes too low to allow this detection. Immersed in water, humans are therefore unable to feel the sound relief. On the other hand, marine mammals such as dolphins emit sounds 10 to 100 times higher than the highest frequency perceived by the human ear. Their wavelength (λ), between 1.5 and 15 cm, is then less than the distance between their ears (about 15 cm). The phase shift between these sounds is then reduced to a significant fraction of the wavelength even when the transmitter is not in line with their ears. It allows them not only to communicate with each other, but also to situate themselves in relation to each other and in relation to any possible obstacles in the darkness of the seabed.
In solid media, sound spreads even faster than in liquids. This is because solids are even less compressible than liquids. Thus, in the anvil steel mentioned at the beginning of this article, the speed is about 5000 m/s. If its length is close to 50 cm, it means that the entire anvil has felt the shock of the hammer in one ten-thousandth of a second, while the sound waves in the neighbouring air take almost 2 milliseconds to travel the same distance. In other words, approximately, it is the entire anvil, and not just the area impacted by the hammer, that emits the sound heard by the blacksmith.
References and notes
Cover image. The acoustic waves emitted by a radially vibrating sphere propagate in all directions in the form of alternating compression and relaxation of the gas layers adjacent to each other. Source: By Thierry Dugnolle (Own work)[CC0], via Wikimedia Commons]
[1] The compressibility of air is both large enough for this fluid medium to carry sound and small enough to justify the use of incompressible approximations to describe aerodynamics at speeds well below the velocity of sound.
[2] The negative electrical charges of the electrons surrounding the nuclei of the hydrogen and oxygen atoms that form the water molecule are subjected to the Coulomb force that strongly pushes them away from each other when their distance becomes very small. In turn, these electrons transmit this repulsive force to atoms and molecules.
[3] The logarithm is the mathematical operation that substitutes an addition for a multiplication: log (ab) =log(a)+log(b). Multiply the sound pressure by 10, the number of which the decimal logarithm is the unit, then results in the addition of a unit to its logarithm. In the usual notations, log10 refers to the decimal logarithm, while Log refers to the naperian logarithm, whose base is the irrational number e = 2.71828..
[4] Name in honour of Graham Bell (1847-1922), Scottish scientist and inventor of the telephone. The decibel (dB) is one-tenth of the Bel, very rarely used.
[5] The range of a sound characterizes its pitch, i.e. its frequency, whether it is a sound produced by an instrument or a human voice. The range of the violin is between 300 and 1400 Hz, that of the cello between 70 and 750 Hz and that of the double bass between 60 and 350 Hz.
[6] A waveguide is a physical system used to confine waves in a particular environment, at least over a certain distance. It is widely used with light and electromagnetic waves in general, for example in optical fibres. In the case of acoustic waves, particularly in seawater, its effectiveness is less clear-cut due to the more fuzzy nature of the interfaces, which do not channel the different wavelengths in the same way.
[7] With a 90-degree orientation difference of emitters A and B in Figure 9, we can therefore associate a 360/20 = 18-degree phase shift with respect to the axis of the human body, for a frequency of 100 Hz for which d/λ=1/20. The ratio 18/90 = 1/5 characterizes the sensitivity of humans to sound relief in the air.
The Encyclopedia of the Environment by the Association des Encyclopédies de l'Environnement et de l'Énergie (www.a3e.fr), contractually linked to the University of Grenoble Alpes and Grenoble INP, and sponsored by the French Academy of Sciences.
To cite this article: MOREAU René (February 7, 2019), The emission, propagation and perception of sound, Encyclopedia of the Environment, Accessed July 27, 2024 [online ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/en/physics/emission-propagation-and-perception-of-sound/.
The articles in the Encyclopedia of the Environment are made available under the terms of the Creative Commons BY-NC-SA license, which authorizes reproduction subject to: citing the source, not making commercial use of them, sharing identical initial conditions, reproducing at each reuse or distribution the mention of this Creative Commons BY-NC-SA license.