Sur les contributions à la physique statistique de Giorgio Parisi, lauréat du prix Nobel 2021
PDF
Trois lauréats se partagent le prix Nobel de physique 2021 pour leurs études de phénomènes complexes. Syukuro Manabe et Klaus Hasselmann ont jeté les bases de notre connaissance du climat de la Terre et de la manière dont l’humanité l’influence. Le troisième lauréat, Giorgio Parisi, est récompensé pour ses contributions révolutionnaires à la théorie des phénomènes désordonnés et aléatoires. Dans cet article, les auteurs Roberto Benzi et Uriel Frisch, proches collaborateurs et amis de Giorgio Parisi, offrent leur vision de deux de ses contributions majeures, auxquelles ils ont respectivement participé. Roberto Benzi explique la contribution de Parisi et de ses collaborateurs à la compréhension conceptuelle des transitions entre climats tempérés et glaciaires. Uriel Frisch aborde l’un des plus vieux problèmes non résolus de la science, concernant la dynamique de la turbulence et sa prolifération de « fractales ». Les contributions des deux autres lauréats sont présentées dans un autre article sous la rubrique « climat ».
1. Un prix Nobel pour des contributions révolutionnaires à la compréhension des systèmes complexes
Alors que le GIEC a reçu le prix Nobel de la paix en 2007, la science du climat est honorée par le prix Nobel de la physique pour la première fois en 2021. Cette science repose sur la mécanique des fluides et les processus thermodynamiques classiques, apparemment loin de la frontière actuelle de la physique. La difficulté vient cependant de l’interaction complexe de ces différents processus, qui se produisent sur une très large gamme d’échelles dans l’espace et le temps.
Parmi les trois lauréats, Syukoro Manabe et Klaus Hasselmann ont été les pionniers de l’approche de modélisation qui a conduit aux modèles climatiques actuels (Lire : Sur les contributions aux sciences du climat de Klaus Hasselmann et Syukuro Manabe, prix Nobel 2021). Cela nécessitait une bonne connaissance de la physique pour évaluer les effets dominants avec une puissance informatique très limitée. Une limitation plus fondamentale est due au comportement instable du système, illustré par la difficulté des prévisions météorologiques, même avec les ordinateurs les plus puissants disponibles aujourd’hui. Cependant, un tel comportement chaotique conduit à des statistiques bien définies sur une longue échelle de temps, comme cela est demandé pour les études climatiques. C’est le domaine de la physique statistique, le champ de recherche auquel Giorgio Parisi a apporté plusieurs contributions importantes.
La physique statistique a été initialement développée pour prédire les propriétés de la matière à partir des premiers principes. Après les contributions pionnières de Ludwig Boltzmann qui a clarifié le concept d’entropie, Albert Einstein et Paul Langevin ont explicité le mouvement brownien des particules colloïdales sous l’effet de collisions moléculaires aléatoires. Klaus Hasselmann a appliqué des approches similaires aux systèmes climatiques, dans lesquels les fluctuations météorologiques rapides remplacent les collisions moléculaires. Giorgio Parisi et ses collègues ont analysé comment de telles fluctuations déclenchent des transitions entre deux états stables, comme indiqué en section 2.
La section 3 traite d’un sujet différent, le vieux problème de la turbulence, une interaction complexe de tourbillons à différentes échelles qui défie la physique et les mathématiques depuis plus d’un siècle. Giorgio Parisi a introduit le concept de multifractales pour rendre compte des données expérimentales.
Notez que ces deux sujets ne sont pas les seules contributions pour lesquelles Giorgio Parisi a reçu le prix Nobel. Son travail le plus célèbre est la théorie des systèmes magnétiques désordonnés, comme l’expliquent les rapports officiels [1] de l’Académie royale suédoise. Ses diverses contributions permettent de mieux comprendre les systèmes complexes au-delà de la physique. Elles influencent également les mathématiques, la biologie, les neurosciences et l’apprentissage automatique. Cette influence a été favorisée par son leadership stimulant et amical auprès des étudiants et des collègues.
2. Résonance stochastique et périodes interglaciaires (par R. Benzi)
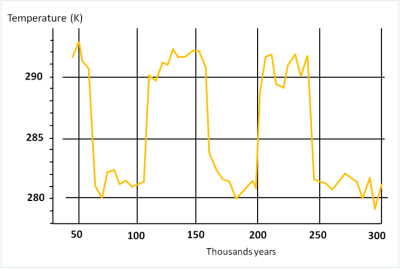
Les scientifiques qui ont analysé la composition de la glace au Groenland et en Antarctique ont fourni les preuves que, au cours du dernier million d’années environ, le climat de la Terre a connu des périodes glaciaires et interglaciaires avec une périodicité d’environ 100 000 ans et une différence de température d’environ 10 degrés. La question de savoir comment expliquer l’alternance quasi-périodique observée du comportement climatique était un défi (Lire Théories astronomiques du climat : une longue histoire).
Pour répondre à cette question, considérons le modèle climatique le plus simple possible qui traite du bilan énergétique global de la Terre (voir figure 1). Le soleil fournit un rayonnement entrant (Rin) qui est partiellement réfléchi (Rout) vers l’espace par la surface de la Terre (glace, nuages et autres effets de surface). Le rayonnement entrant net Rin–Rout réchauffe la surface de la Terre qui émet un rayonnement infrarouge. En connaissant ce rayonnement entrant net, on peut estimer la température du sol (à l’échelle mondiale) en utilisant nos connaissances sur la façon dont l’émission radiative dépend de la température. Dans un état stationnaire, ce rayonnement infrarouge équilibre simplement le rayonnement entrant net Rin–Rout. On obtient ainsi une assez bonne estimation de la température moyenne globale de la Terre correspondant à la période interglaciaire actuelle, soit environ 15 degrés Celsius (Lire : La température moyenne de la Terre).
Bien que le flux infrarouge émis soit partiellement absorbé par les gaz à effet de serre dans l’atmosphère, l’émission nette est une fonction croissante de la température, proche de l’expression du corps noir en Rin-Rout (Lire : Le rayonnement thermique du corps noir). Ceci est schématisé comme une fonction linéaire de la température T dans la figure 2. Quant au rayonnement réfléchi, il dépend fortement de la surface couverte par la neige, qui réfléchit la lumière plus efficacement que le sol et l’eau libre. Par conséquent, le flux entrant Rin–Rout augmente également avec la température. Comme l’ont montré Budyko [2] et Sellers, cette augmentation est forte avec la fonte des grandes calottes glaciaires d’Amérique du Nord et d’Eurasie. Il en résulte la courbe noire présentée sur la figure 2.
Les états stationnaires correspondent aux trois intersections des deux courbes. Le point central représente cependant un état instable : une petite augmentation de la température à partir de ce point stationnaire conduit en effet à un excès de rayonnement entrant Rin–Rout, entraînant une nouvelle augmentation de la température, jusqu’à ce que le système atteigne le point stable chaud. De même, une légère baisse de température est amplifiée et conduit au point stable froid représentant un climat glaciaire. Ce modèle fournit donc une explication conceptuelle simple de deux états stables. Dans le modèle original de Budyko-Sellers, l’état glaciaire fait référence à une Terre recouverte de glace. Il correspond à une température extrêmement basse, jamais observée dans les enregistrements paléoclimatiques des derniers millions d’années.
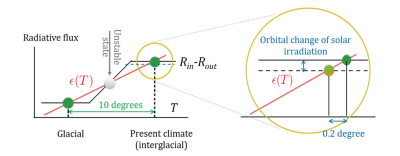
À première vue, on peut penser que le cycle de Milanković est capable d’expliquer le comportement presque périodique observé dans les enregistrements paléoclimatiques. Cependant, un problème majeur a laissé les scientifiques perplexes pendant des décennies : le fait est que les fluctuations de Milanković dans le rayonnement solaire entrant étaient extrêmement faibles, de l’ordre de 0,1 %. Cette très faible modulation du Rin-Rout entraînerait une modulation de la température d’environ 0,2 degré, bien plus faible que la différence de température enregistrée entre les états glaciaires et interglaciaires.
Au début des années 80, Giorgio Parisi et ses collègues ont développé une nouvelle approche théorique pour résoudre cette énigme [3]. Le point de départ était à nouveau le bilan énergétique de surface considéré précédemment. Ensuite, en examinant les relevés climatiques et les modèles de circulation numérique, ils ont compris que la température moyenne de la Terre fluctue d’année en année en raison de la dynamique interne et non linéaire du climat. Le point crucial était de considérer ces fluctuations comme du «bruit» et en particulier du «bruit interne» intégré à la dynamique du climat. Parisi et ses collègues ont poursuivi cette idée et ont observé que s’il existe deux états climatiques avec une différence de température d’environ 10 degrés, le climat de la Terre, en raison des fluctuations climatiques internes, peut présenter une excursion aléatoire d’un état à l’autre. Cela se produirait en moyenne une fois tous les 50 000 ans si les deux états correspondent aux états glaciaires et interglaciaires observés. Cela correspond à l’intervalle typique de 50 000 ans entre les transitions, mais sans la véritable périodicité observée dans les enregistrements paléoclimatiques.
L’existence de deux états peut être comprise, encore une fois, comme le changement de la réflexion de la surface de la Terre en fonction de la température : lorsque la température diminue, il n’est pas difficile d’imaginer une augmentation de la couverture de glace et de nuages dans le climat et un état climatique d’équilibre peut être atteint.
Outre le point hautement non trivial concernant l’existence de deux états climatiques (glaciaire et interglaciaire), la théorie proposée par Parisi et ses collaborateurs repose sur deux concepts fondamentaux : les effets du bruit sur de longues échelles de temps et la coopération renforçant le bruit.
Pour la première fois dans les théories climatiques, le bruit fournit le mécanisme moteur du changement climatique sur des échelles de temps très longues. Dans le domaine du climat, ce que nous appelons bruit est l’effet des variables climatiques non linéaires à petite échelle sur les variables dites «macroscopiques», comme la température globale de la Terre. Il existe désormais des exemples quantitatifs bien définis qui nous permettent de parler de bruit, même si le mot en lui-même peut être trompeur. L’effet du bruit amène tout système à effectuer des fluctuations autour d’un état stable (s’il existe). Cependant, si le système est non linéaire et qu’il existe plus d’un état stable, le bruit, avec une petite probabilité exponentielle, peut faire passer le système d’un état à un autre. Bien que faible, sur une très longue échelle de temps, comme dans le cas du climat, cela conduit à nune transition aléatoire (non périodique) entre les états.
Le deuxième point, à savoir les effets coopératifs du bruit et du forçage externe, était entièrement nouveau en physique et pas seulement chez les théoriciens du climat : personne n’avait jamais pensé à cette possibilité. L’article [3] de Parisi et ses collègues montre pour la première fois que cette coopération peut se produire dans un système non linéaire comme le climat de la Terre. Plus tard, cet effet coopératif a été généralisé pour les systèmes chaotiques [4] et, à l’heure actuelle, il existe des milliers d’applications qui exploitent le mécanisme de résonance stochastique en physique, en biologie et dans d’autres recherches scientifiques.
3. Modèles multifractaux pour la turbulence (par U. Frisch)

Nous commençons ici par la contribution la plus ancienne, directement liée au travail de Giorgio Parisi, à savoir celle d’A.N. Kolmogorov (1941) [5], abrégée en K41. Elle traite de la « turbulence pleinement développée », ce qui signifie que les tourbillons peuvent interagir librement sur une large gamme d’échelles. Ces interactions transfèrent de l’énergie aux très petits tourbillons, qui sont amortis par la viscosité. Cette cascade d’énergie est en jeu, par exemple, dans le processus de traînée turbulente (Lire : Traînée subie par les corps en mouvement). Les caractéristiques spécifiques de l’écoulement aux plus grandes échelles sont brouillées par les interactions turbulentes grâce à ce processus en cascade. Kolmogorov a alors observé que le fait d’ignorer complètement la viscosité pouvait conduire à une équation dynamique dans laquelle les tourbillons de plus en plus petits seraient simplement similaires – au sens statistique – à ceux qui gouvernent les tourbillons plus grands. Le niveau correct de similarité est déterminé en exigeant un taux de dissipation d’énergie fini lorsque la viscosité tend vers zéro. Cette image autosimilaire (cf. figure 5a) a connu un succès étonnant.
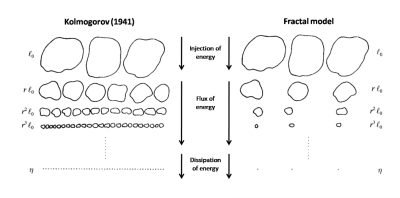
Bien que Kolmogorov soit avant tout un mathématicien, l’un des plus grands du 20e siècle, il a voulu confirmer sa théorie par des données expérimentales recueillies dans son laboratoire de Moscou et dans les environs. Ces travaux ont fourni des preuves solides que la turbulence est loin de l’image autosimilaire décrite ci-dessus : les petits tourbillons remplissent beaucoup moins l’espace que les plus grands et présentent une intermittence (cf. figure 5b). Cela a conduit Kolmogorov et ses collaborateurs à proposer un modèle d’intermittence en 1961 [6].
Un phénomène d’intermittence avait également été découvert par G.K. Batchelor et A.A. Townsend (1949) [7] et la question s’est posée de savoir si ce phénomène serait ou non compatible avec l’image autosimilaire de K41. Pour décrire l’intermittence de Kolmogorov, B. Mandelbrot (1974) [8] a proposé d’utiliser son modèle « fractal » . Les fractales sont des objets géométriques obtenus par l’insertion itérative d’un motif similaire à des échelles de plus en plus petites. Les mathématiciens avaient introduit ce concept dès la fin du 19e siècle. En 1950, L.F. Richardson, un autre géant de la turbulence et de la dynamique atmosphérique, a utilisé les fractales dans un tout autre contexte, à savoir comment éviter les conflits entre nations. Il semble qu’une frontière fractale convoluée entre pays sera en effet plus encline à développer des conflits qu’une frontière plus droite.
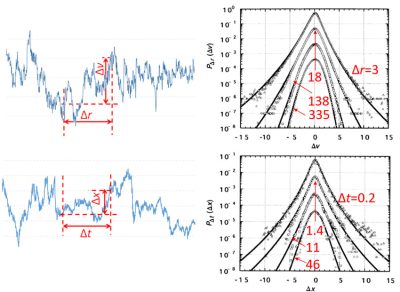
Pour appréhender la structure multi-échelle du signal, une approche naturelle consiste à étudier la différence de vitesse Δv entre deux points séparés par une distance donnée Δr. La variance (la moyenne de |Δv|2) indique comment l’énergie est distribuée [9] entre les différentes échelles. Cependant, la variance ne décrit pas tout : elle ne permet pas de distinguer les tourbillons rares et intenses des tourbillons qui remplissent l’espace avec la même énergie globale. Une telle information est fournie par les distributions de probabilité (histogrammes) présentées dans la partie droite de la figure 6. Les longues « queues » de ces histogrammes représentent des événements rares et intenses. Celles-ci deviennent plus fortes pour une petite séparation Δr, révélant que les petits tourbillons sont plutôt épars. C’est l’essence même de l’intermittence. Une analyse similaire peut être effectuée pour toute série temporelle en considérant un intervalle de temps Δt au lieu d’une distance, comme le montre la figure 6 pour un marché financier. Les queues représentent alors la probabilité d’une forte baisse ou d’une forte hausse dans un intervalle de temps donné, ce qui présente un intérêt direct pour la gestion des risques.
Pour revenir à la turbulence, ces queues peuvent être évaluées en considérant la moyenne de |Δv|p (le moment d’ordre p). Celles-ci sont en effet d’autant plus sensibles aux grandes fluctuations que leur ordre p est élevé. Leur dépendance vis-à-vis de la séparation Δr, appelée fonctions de structure, caractérise donc l’intermittence. Dans la cascade réellement autosimilaire décrite par K41, la fonction de structure d’ordre p se comporte comme la loi de puissance |Δr|p/3 (figure 7). Les expériences indiquent une loi de puissance |Δr|ζ(p) avec des exposants ζ(p) plus petits que p/3: les moments élevés sont relativement plus forts dans la limite de la petite séparation Δr, ce qui caractérise l’intermittence.
Le modèle proposé par Kolmogorov en 1961 est plus proche des résultats expérimentaux, mais il conduit à une diminution de ζ(p) pour un grand indice p qui s’avère être mathématiquement incohérent. Comme alternative, des modèles fractals ayant un certain contact avec les équations dynamiques de la turbulence ont été introduits, notamment par Frisch, Sulem et Nelkin (1978) [10]. Cela donne une augmentation linéaire de ζ(p) avec p, avec une pente inférieure à 1/3. La pente dépend d’un seul paramètre, relié à la dimension fractale, qui quantifie la façon dont les tourbillons actifs deviennent de plus en plus épars à des échelles de plus en plus petites. Les expériences révèlent cependant une courbe convexe, comme le montre la figure 7.
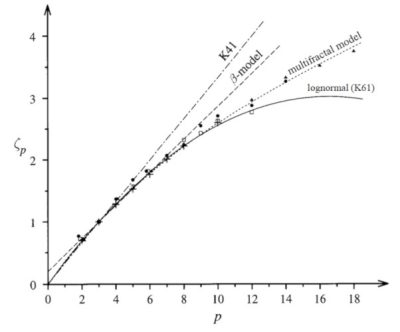
Durant l’été 1983, G. Parisi et U. Frisch ont participé à une école d’été à Varenna (Italie) sur le thème «Turbulence et prévisibilité dans la dynamique des fluides géophysiques et la dynamique du climat» Les données expérimentales de F. Anselmet, Y. Gagne, E.J. Hopfinger, R.A. Antonia [11] étaient difficilement compatibles avec une seule fractale, comme le montre la figure 7. Avec une remarquable intuition physique, G. Parisi a proposé un modèle multifractal pour rendre compte de ces résultats. Cet accord avec l’expériece dépend de paramètres d’ajustement mais l’analyse sous-jacente a révélé des propriétés mathématiques profondes.
Cette idée d’avoir plus d’une dimension fractale – voire une infinité de dimensions fractales – trouve son origine dans un sujet très difficile : l’évaluation du grand risque ou de la ruine financière. Les travaux pionniers ont été réalisés par un mathématicien suédois, H. Cramér (1938) [12], qui avait une solide expérience de la finance. La vision standard avant Cramér était que, en ajoutant n variables aléatoires indépendantes et également distribuées, on obtiendrait (avec des conditions appropriées) deux propriétés majeures : la moyenne tendrait vers la moyenne (loi des grands nombres), et les déviations de la moyenne, divisée par n1/2, tendraient vers une loi gaussienne (le théorème de la limite centrale).
Mais que se passe-t-il lorsque l’on multiplie les variables au lieu de les additionner (ou de manière équivalente lorsque l’on additionne des variables et que l’on prend une exponentielle du résultat) ? C’est précisément ce qui se passe dans la pulvérisation des roches, un problème étudié par Kolmogorov [13] avant que les résultats de Cramér ne soient bien connus. La probabilité d’une granulométrie donnée résulte en effet d’un produit de probabilités d’événements de rupture successifs et indépendants. Il est alors exceptionnel d’obtenir des limites gaussiennes. Tous ces problèmes font intervenir une fonction étrange appelée fonction de grande déviation, qui caractérise l’écart à la loi des grands nombres. Son nom change selon les domaines : «la fonction de taux», «la fonction de Cramér» ou encore «l’entropie». Oui, l’entropie de Boltzmann n’est qu’un cas particulier ; comprendre l’entropie, sans aucune théorie avancée des probabilités est remarquable, à moins d’être Boltzmann.
Voici quelques références clés sur les multifractales. La référence initiale est en fait une annexe de 2,5 pages par Parisi et Frisch à un article de Frisch [14] publié dans les actes de la réunion de Varenna en 1983. Immédiatement après, un article plus détaillé a été rédigé par Benzi, Paladin, Parisi et Vulpiani [15]. Il comprenait une extension cruciale de la turbulence pleinement développée à l’attracteur étrange dans les systèmes dynamiques chaotiques. L’argument clé de ces articles des années 80 fait appel à la transformation de Legendre, la même transformation qui apparaît en thermodynamique statistique lors de la définition de l’entropie, mais les grandes déviations de Cramér ne sont pas mentionnées. Une présentation beaucoup plus détaillée, centrée sur une présentation élémentaire des grandes déviations, se trouve dans le livre de Frisch (1995) [16]. Enfin, il existe un excellent texte en ligne d’Yves Meyer (2021) [17], qui est en principe destiné aux mathématiciens, mais qui peut être lu aussi par des personnes sans connaissances mathématiques avancées.

Enfin, nous voulons souligner un paradoxe. Il est clair que des mesures de plus en plus précises de l’écoulement turbulent ont été un moteur du développement de l’analyse multifractale. Il existe quelques théorèmes rigoureux [18] concernant les singularités multifractales apparaissant dans les équations modèles. Néanmoins, nous ne disposons pas d’un seul théorème prouvé applicable aux équations de Navier-Stokes qui décrit une turbulence développée tridimensionnelle (3D). Malgré cette base mathématique précaire, l’analyse multifractale est maintenant couramment utilisée pour analyser quantitativement une grande variété de phénomènes chaotiques ou turbulents complexes observés dans l’environnement, comme les enregistrements temporels climatiques, les rafales de vent, les formes des nuages, le vent solaire.
4. Messages à retenir
- Giorgio Parisi a reçu le prix Nobel de physique en 2021 pour ses contributions de premier plan à des avancées majeures en physique statistique.
- Deux de ces contributions sont pertinentes pour les flux climatiques et environnementaux. Il s’agit des concepts de «résonance stochastique» et de «multifractales» ;
- La résonance stochastique est un effet coopératif du bruit et d’un forçage périodique externe qui peut conduire à une commutation quasi périodique entre deux états stables. Elle a été initialement proposée comme modèle conceptuel pour les enregistrements paléoclimatiques du dernier million d’années, mais elle s’est avérée avoir de nombreuses applications en physique, en biologie et dans d’autres domaines scientifiques ;
- Les multifractales ont été introduites pour décrire la structure multi-échelle observée dans les écoulements turbulents. Le concept s’est avéré très pertinent pour d’autres systèmes chaotiques et a suscité des progrès dans l’analyse mathématique des processus aléatoires.
Notes et références
Image de couverture. Les trois lauréats du prix Nobel de physique, de gauche à droite, Syukuro Manabe, Klauss Hasselmann, Giorgio Parisi [Source : © illustration Niklas Elmehed, Nobel Prize Outreach]
[1] Article de vulgarisation scientifique : https://www.nobelprize.org/uploads/2021/10/popular-physicsprize2021.pdf, version de plus haut niveau : https://www.nobelprize.org/uploads/2021/10/sciback_fy_en_21.pdf
[2] Budyko, M. I. (1969) « The effect of solar radiation variations on the climate of the earth » Tellus 21, 611-619.
[3] Benzi R., Parisi G., Sutera A., Vulpiani A.. (1982) « Stochastic resonance in climatic change », Tellus 34, 10-16.
[4] Benzi R., Sutera A., Vulpiani A.. (1981) « The mechanism of stochastic resonance », J. Phys. A : Math. Gen. 14, L453-457.
[5] Kolmogorov, A.N. (1941a) « The local structure of turbulence in incompressible viscous fluid for very large Reynolds number ». Dokl. Akad. Nauk SSSR 30, 9-13 (traduit dans Proc. R. Soc. Lond. A 434, 9-13 (1991)).
[6] Kolmogorov, A.N. (1961) « Précisions sur la structure locale de la turbulence dans une fluide visqueux aux nombres de Reynolds élevés », in « La Turbulence en Mécanique des Fluides », 447-451, eds. A. Favre, L.S.G. Kovasznay, R. Dumas, J. Gaviglio & M. Coantic. Gauthiers-Villard, Paris. Une traduction anglaise peut être trouvée dans Kolmogorov, A.N. (1962) J. Fluid Mech. 13, 82 – 85.
[7] Batchelor, G.K et Townsend, A.A. (1949) « The nature of turbulent motion at large wave-numbers ». Proc. R. Soc. Lond. A 199, 238-255.
[8] Mandelbrot, B. (1974) « Intermittent turbulence in self-similar cascades : divergence of high moments and dimension of the carrier ». J. Fluid Mech. 62, 331-358.
[9] Cette variance est liée au «spectre d’énergie» qui peut être obtenu également à partir de la transformée de Fourier du signal.
[10] Frisch, U., Sulem, P.L. et Nelkin, M (1978) « A simple dynamical model of intermittent fully developed turbulence ». J. Fluid Mech. 736, 5-23.
[11] Anselmet, F., Gagne, Y., Hopfinger, E.J. et Antonia, R.A. (1984) « High-order velocity structure function in turbulent shear flow ». J. Fluid Mech. 140, 63-89.
[12] Cramér, H. (1938) « Sur un nouveau théorème-limite de la théorie des probabilités », Actualités Scientifiques et Industrielle 736, 5-23.
[13] Kolmogorov, A.N. (1941) « On the logarithmic normal law of distribution of the size of particles under pulverization » Dokl. Akad Nauk SSSR 31, 99-101.
[14] Parisi, G. et Frisch, U. (1985) On the singularity structure of fully developed turbulence, in Turbulence and Predictability in Geophysical Fluid Dynamics. Proceed Intern. School of Physics ‘E. Fermi’. 1983. Varenna. Italy, 84-87. Il s’agit d’une annexe à l’article ‘Fully Developed Turbulence and Intermittency’ de Frisch, U. pp. 71-88.
[15] Benzi, Paladin, Parisi et Vulpiani (1984) « On the multifractal nature of fully developed turbulence and chaotic systems », J. Phys. A : Math. Gen. 17, 3521.
[16] Frisch, U. (1995) « Turbulence, the Legacy of A.N. Kolmogorov », Cambridge University Press.
[17] Meyer, Y. (2021) « Giorgio Parisi et la turbulence », Disponible en français sur le site de l’Institut national des sciences mathématiques et de leurs interactions https://www.insmi.cnrs.fr/fr/cnrsinfo/giorgio-parisi-et-la-turbulence-par-yves-meyer.
[18] Jaffard, S. (2000) « On the Frisch-Parisi conjecture », J. Math. Pures Appl. 69, 6, 525-552.
L’Encyclopédie de l’environnement est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.
Pour citer cet article : BENZI Roberto, FRISCH Uriel (6 janvier 2022), Sur les contributions à la physique statistique de Giorgio Parisi, lauréat du prix Nobel 2021, Encyclopédie de l’Environnement. Consulté le 1 mai 2024 [en ligne ISSN 2555-0950] url : https://www.encyclopedie-environnement.org/physique/prix-nobel-physique-2021/.
Les articles de l’Encyclopédie de l'environnement sont mis à disposition selon les termes de la licence Creative Commons BY-NC-SA qui autorise la reproduction sous réserve de : citer la source, ne pas en faire une utilisation commerciale, partager des conditions initiales à l’identique, reproduire à chaque réutilisation ou distribution la mention de cette licence Creative Commons BY-NC-SA.







