Stratification and instabilities in natural fluid environments

What is the relationship between a fog layer, a rainbow cocktail or piles of geological layers? These structures are all superimpositions of distinct layers, like a yarrow! The air in the atmosphere, the water in lakes or oceans and colourful cocktails are fluid media subject to gravity. When they are in equilibrium, the heaviest parts are located at the bottom, the lightest parts at the top, this separation can give rise to a stratification phenomenon. But things get more complicated when instabilities set these fluids in motion. Meteorology, climatology and the dispersion of pollutants find serious challenges here.

1. Fluids at rest… almost

It is the law of hydrostatics that governs the state of equilibrium of a fluid structure at rest. It requires that the pressure decreases with altitude so that, at the bottom of a horizontal layer, the pressure is higher than at the top. The difference between these pressures leads to an upward vertical force exactly opposite to the weight of the fluid layer. The article Pressure, temperature and heat is a reminder of this equilibrium of a fluid at rest, of the origin of the pressure forces capable of compensating for the weight of a layer of this fluid and of this law of hydrostatics.

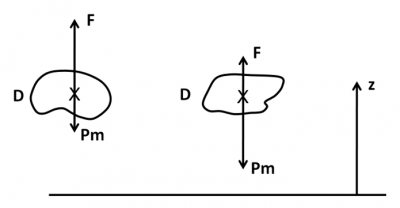
Let us imagine a small area within the fluid medium, of any shape and of volume V. It can be occupied by the fluid itself, by another fluid, or by a solid body. The resultant of the pressure forces exerted by the external medium on the surface of this domain is a vertical force, directed upwards: Archimedes’ thrust. Its value F is given by the formula F = ρgV, where ρ is the density of the fluid and g is gravity. It is exactly the weight P of the “displaced fluid“, i.e. the fluid that should occupy the volume V.

The medium in domain D in Figure 1 also has its own weight Pm, directed downwards. This domain is therefore subject to both:

• to the Archimedes Thrust F facing upwards,
• at its weight Pm pointing downwards.

The resultant of these two forces is the apparent weight of the D domain: Pa = F – Pm. If this apparent weight is negative, and thus directed downwards, Pm prevails and D tends to descend. If Archimedes’ thrust is the strongest, this apparent weight is directed upwards; this imposes the ascent of D. Thus, any fluid mass which is not subject to other constraints evolves towards a state of stable equilibrium, where the heaviest parts are at the bottom, the lightest at the top. But we will see in the next section that there are limits to this selection by density.

There are various reasons why the density may vary within the fluid. Temperature can cause expansion of portions of the fluid range. In addition, fluids such as air and water are mixtures and are rarely homogeneous in composition. These variations always result in certain portions of the fluid range becoming lighter or heavier and moving within the surrounding environment. We can observe this rise above the radiators of heated apartments, but also outside when smoke comes out of chimneys. Similarly, in certain Mediterranean volcanic regions, where the deep water is warmer than that of the surface layers, upward currents are produced locally and are often sought after by bathers and some curists. Conversely, these mechanisms can impose dives to the depths for portions heavier than the surrounding fluid.

The presence of airborne particles or droplets, known as aerosols, is another example of local variation in density.

• In the air, it often appears as patches of mist or fog, apparently lying on bodies of water or fields (Figure 2).
• In ponds and lakes, suspended sludge tends to sink to the bottom where it forms layers of silt.
• In the oceans, which are subject to such a slow global circulation that the law of hydrostatics may apply, a phenomenon such as the plunge of the Gulf Stream in the vicinity of Greenland can be explained by the fact that its waters become heavier than their environment because they are both colder and saltier (read: The slow and powerful ocean circulation).

2. Stratification under the influence of gravity

Gravity thus imposes a steady state in resting fluids where density decreases with altitude. Strictly speaking, we speak of stratification when a real discontinuity appears between two fluid layers, as in the cocktails in the introductory image [1]. Density is the state variable [2] most directly involved since it is the one whose value can undergo a real jump imposed by gravity. The concentration of a particular species, when it causes this discontinuity, also undergoes this jump, clearly illustrated by the change of colour in cocktails, linked to a change in density. In the atmosphere, the presence of a sea of clouds that mountain hikers can observe from above is another example. But pressure and temperature, other variables characteristic of the state of the fluid, cannot undergo a jump; only their derivatives along the vertical can experience such a discontinuity, also linked to the change in density of the fluid.

It should be noted, however, that the influence of pressure on the density of water is practically negligible compared to the influence of temperature, which justifies the fact that water is often considered incompressible, whereas it is quite expandable. Typical values for its compressibility and expandability are 4. 10-10 Pa-1 and 2. 10-4 K-1, respectively. More concretely, these values mean that in order to vary the density of water by 0.1%, a temperature difference of 5°C is sufficient, whereas a pressure difference of 20 times atmospheric pressure, i.e. a depth difference of 200 m, is required to achieve the same 0.1% variation.

3. A few examples

Apart from those mentioned above, there are many examples of stratification of liquid media. When preparing a dressing, if the oil is poured slowly enough over the vinegar, it is observed that it floats on the surface and that vigorous agitation of the mixture is necessary to destroy this stratification, which would eventually recover. The formation of a fairly homogeneous café au lait usually requires stirring the mixture. The foams of beer or champagne, even if they are not pure liquids, also illustrate the fact that this stratification is the only possible stable state of these drinks, as long as the foam lasts.

At sea, the settling of solid particles is at the origin of the formation of sediments, whose signature in the limestone rocks is visible on Figures 3 and 4. Quite easy to date using Carbon 14 radioactivity, it is an essential means available to geologists to reconstruct the history of the earth’s crust and that of the species that inhabited it at the time of sedimentation, now fossilised. The case of the Sassenage fault fold (Figure 4) reveals the succession of sedimentation phenomena, now transformed into layers of hard limestone rocks of different ages, separated by softer, less steep marls, on which vegetation develops. The curvature of these limestone strata and their fractures are evidence of the powerful stresses they underwent during the formation of the Alpine massif (Read: The origin of life as seen by a geologist who loves astronomy).

The surface vicinity of lakes, seas and oceans, subject to sunshine, sees its temperature rise from spring to late summer. Since it lightens the upper parts, this heating is stable. However, this surface layer is constantly agitated by the waves, by the associated turbulence, but also by the tides in the case of the oceans. This agitation produces a good mixing and uniformity of temperature to a depth of the same order of magnitude as the wavelength of the waves: a few meters in lakes, several tens of meters in the oceans.

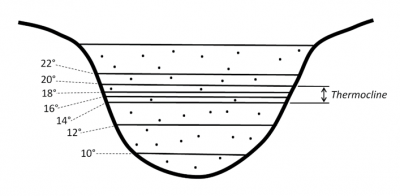
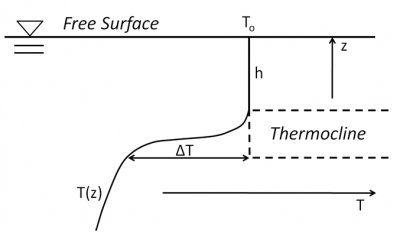
On the contrary, at depth, reduced to pure conduction in a quasi-immobile environment, heat exchanges are very low so that the temperature remains almost invariable. Between these two zones, there is a rather thin zone called the thermocline, where the temperature can vary by about ten degrees (Figures 5 and 6). The temperature of the water above the thermocline experiences significant seasonal variations due to variations in sunlight, while the temperature of the deep layers does not vary. See Figure 2 in the article The Marine Environment.

4. Decanting and stratification have limitations

Some air pollutant particles, especially fine (PM2.5) and ultrafine (PM0.1) particles, remain in suspension for a very long time, to such an extent that they are very difficult to extract (Read: Air Polluting Particles: What are they?). In mists and fogs, very small droplets remain suspended until they evaporate. On the contrary, in clouds darker than summer cumulus clouds, larger hydrometeors [3] precipitate and feed rain, snow or hail (Read: What happens in clouds?). Yet all these objects are subject to the same gravity. So what are the mechanisms that prevent the smaller ones from falling?

First, when a water droplet or a grain of dust falls into the surrounding air, due to its apparent weight, it takes the place of the air below it, and this air must rise above it.

• This object, a droplet or grain, is then subjected to an upward friction force over its entire surface, which is proportional to the square of its mean radius (r2).
• On the contrary, its apparent weight is proportional to the volume, i.e. the cube of its mean radius (r3).

On large enough objects, the competition between these opposing forces is decided in favour of weight, which forces the object to fall. But when the radius r becomes very small, the competition between these forces is won by friction, which prevents the object from falling. In practice, for polluting particles in the air as well as for droplets in fog, the critical radius below which objects can no longer settle is of the order of ten microns.

In sludge, suspended solid particles are subject to the same competition, but the density of these particles is quite close to that of water. As a result, the critical radius is much larger, of the order of a hundred microns.

Other mechanisms also help to prevent the stable suspension of very small objects. One of them is Brownian motion, which is analogous to the agitation of molecules, although it is much less intense at the micron scale than at the nanometer scale (Read: Diffusion, the ultimate step in good mixing). This motion causes each object to collide with many surrounding particles and molecules, giving it an effective cross-section much larger than its radius, and requiring larger passage sections for its trajectory.

5. When instabilities arise

Fluid domains heated from below can become unstable when the temperature difference between the bottom and the surface exceeds a critical threshold. This is the Rayleigh-Taylor instability [4]. This critical threshold is very low in the case of the lower layers of the Earth’s atmosphere. It is this instability which, in periods of very calm high pressure, after a complete night’s rest and in the absence of wind, systematically creates air agitation as soon as the sun rises, which agitates the leaves and makes the flags flutter.

In water, this instability is easy to observe as soon as a container is placed on the fire. It is then influenced by th

e geometry of the vessel, with the liquid rising along walls that are hotter than the inner liquid, and falling back down in the central part.

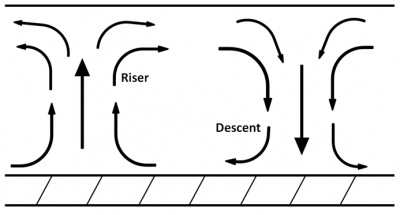
Under more controlled conditions, such as some laboratory experiments where the depth of the liquid layer is much less than its horizontal extent, the formation of cells with a horizontal dimension close to the depth is observed. These cells, which are generally identical, are animated by a well-organized convection movement. The liquid rises on one side, in a kind of chimney, and descends on the other in a kind of well (Figure 7). In the chimney the apparent weight Pa of the liquid is directed upwards, while it is directed downwards in the well. Together these two forces form a torque which may be able to set the entire cell in motion, despite the braking provided by the viscosity of the liquid.

Video 1: Instability of Rayleigh-Taylor and its characteristic “mushrooms” illustrated with hot coloured water injected into cold water. [Source: Jens Niemeyer]

The organization of the convective cell array depends strongly on the geometrical parameters of the experiment. It can be a very regular hexagonal array, especially when the upper plane is a free surface. Between two solid walls forming a parallelepipedic cavity, one can rather observe parallel rollers. In nature very varied situations can be observed.

Video 2: Rayleigh-Bénard convective cells in heated oil mixed with small aluminium particles.

6. Some geophysical examples of convection

6.1. Thawing of the tundra

In the Arctic regions, the ground remains frozen deep all year round, forming what is called permafrost. Only a thin surface layer thaws in summer under the influence of sunlight. With global warming, however, we are beginning to observe a deep thaw here and there, which may be accompanied by convective movements. The photograph in Figure 8, taken in Siberia during the summer of 2019, shows a typical example: convective cells that are roughly rectangular and bounded by earth ridges.

The phenomenon seems to be explained as follows: an earthy soil that thaws becomes a mud, certainly thick, but fluid, especially below 4°C, the temperature at which the density of water reaches its maximum. The mud at the bottom, in contact with the ground still frozen at 0 or 1°C, is therefore lighter than the mud at the surface, at least when it does not exceed 7°C (water at 7°C has the same density as water at 1°C). A network of chimneys can therefore be formed where the lighter mud will rise from the bottom. But in the vicinity of wells, the water it contains tends to fall back to the bottom, leaving these dried-up bulges on the surface. At the scale of each cell there is then a layer of almost pure water, covering the mud that returns to the bottom. Here, the stirring causes a real separation of the liquid and solid phases in an initially homogeneous medium.

6.2. Navigating a volcano

There are a very small number of volcanoes on Earth whose crater contains a permanent lava lake. The largest is that of Nyiragongo, in Central Africa, with a diameter of nearly 250 m (Figure 9). This size allows the observation of a large number of relatively stable convective cells, which form a spider web network. Their shape is irregular, but approximately polygonal. The red lines in Figure 10 show the areas where the hot lava rises from the bottom. On contact with air, it cools and takes on a dark hue. The dark areas are the wells through which the lava returns to the bottom.

One can be surprised by the fineness of the red lines in Figure 10: their surface is much smaller than that of the descending areas. The reason for this is the considerable variation in the viscosity of the lava near its melting point: around 1400°C, it is very fluid; as soon as it has lost 50 or 100°, it becomes pasty and its viscosity is multiplied by 100. As a result, its movement is much slower than that of the rising lava. The rising flow rate being equal to the descending flow rate, if V is the speed of the fluid, and S is the passage section, the flow rate is SV and its conservation imposes the equality SV_ascending = SV_descending. The sections are thus in the inverse ratio of the velocities: at much lower velocity, much larger section.

6.3. The particular case of the Erta Ale

A small lava lake is still present in the crater of this lake in Ethiopia. Following its eruption in 2017, another crater temporarily formed a few kilometres from the main crater, but with a very different behaviour, as it was traversed by a lava flow that escaped through a spillway visible at the left end of Figure 11. It was a sudden collapse of part of the cliff surrounding the lake that abruptly formed a natural dam and closed off this outlet. The formation of this obstacle caused both a standing wave train between the dam and the crater over the entire surface of the lake and the formation of convective cells. Here too, the clear areas are made up of hot lava from the bottom. The convective cells are roughly rectangular.

When the dam collapsed, the waves disappeared and the flow towards the outlet was restored. This flow caused the convective cells to elongate to the left, as shown in the photograph in Figure 12. The clear lines, corresponding to lava upwelling, oriented in the direction of flow became almost linear. They show that convective motions remain in the presence of the flow.

7. Messages to remember

• In all geophysical fluids gravity imposes a variation in density, decreasing with altitude.
• Stratification is manifested by jumps in density, giving rise to layers of material of different densities, such as fog in the air or mud on the bottom of lakes or seas.
• In large water basins, sunlight causes the seasonal formation of a thermocline, which separates a warm, light surface layer from deep water whose temperature remains almost invariant.
• Very small airborne objects, such as liquid droplets or fine particles, cannot settle due to the friction of the surrounding fluid, which would outweigh their apparent weight.
• Hydrodynamic instabilities, especially in fluids heated from below, can destroy certain equilibriums and oppose possible stratification.
• The lava present in some volcanic craters is also a natural fluid. Variations in temperature induce strong variations in viscosity that give rise to remarkable convective structures.

---

Notes and References

Cover image.

[1] Pedlosky J., Geophysical fluid Dynamics, Springer-Verlag,^2nd edition, 1987

[2] A state variable is any quantity, such as density, pressure, temperature and concentration of each species in a mixture, that characterizes the equilibrium in which the fluid is in equilibrium. These quantities are related by the equation of state of the fluid.

[3] Hydrometeors are airborne objects made up of sets of water drops or ice particles suspended in the air: rain, drizzle, snow, hail, fog.

[4] Drazin P. G. and Reid W. H., Hydrodynamic stability, Cambridge University Press, 1981