Inversion layer, fog and other curiosities of the lower atmosphere

How can we explain that in February-March, in the presence of a beautiful anticyclone, it is warmer at altitude than at the bottom of the valleys covered by a real sea of clouds? This situation, contrary to the law of the standard atmosphere according to which the air temperature decreases linearly with altitude, can be attributed to the presence of an inversion layer. But what is it? What mechanisms make it appear, what parameters control it and what are the consequences? We will see that this inversion layer can be located on the ground or at altitude, that it causes the formation of fogs and that it has other less well known effects, such as an increase in the range of the sound or electromagnetic waves that it manages to channel near the ground.

1. What is an inversion layer?

Within the troposphere, in the presence of a high pressure system, conditions are generally very close to those of the standard atmosphere: while air pressure and density decrease exponentially with altitude, the temperature decreases linearly by 6.5°C per kilometre (Read: The Earth’s atmosphere and gas envelope). This decrease is due to the fact that the Earth’s surface, heated by solar radiation, transmits this heat to the surrounding air by conduction and convection, which means that the temperature gradually decreases with altitude [1].

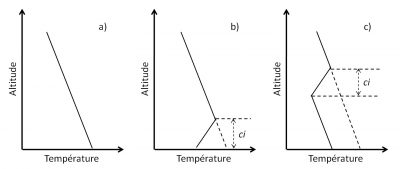
However, exceptions to this 6.5°C/km decrease are quite frequent and lead to the formation of inversion layers where, locally, the temperature can increase as a function of altitude by several degrees (Figure 1). The thickness of these layers is quite variable, from a few tens to several hundred metres, but their horizontal extent is very long, which justifies the use of the word “layer”. Their altitude is also variable, from the ground when they are formed at its contact, to intermediate altitudes between the ground and peaks in mountainous regions. The thickness of these layers and the altitude at which they are formed are highly dependent on the mechanism that leads to their formation.

Within an inversion layer, since the air at the bottom is colder than the air at the top, it is also heavier. As a result, these layers are very stable, i.e. free of convective motion and turbulence. This stability justifies that they are often considered as a kind of cover that prevents any significant upward transport of species or particles accumulated below them, such as pollens, chemical pollutants and air polluting particles.

2. The inversion layer on the soil surface

Every night, deprived of sunlight, the surface of the ground or bodies of water cools by infrared radiation towards space. The air in contact with them, which is colder and heavier than the air above, has no tendency to rise. The very low atmosphere thus regains the rest it had given up at sunrise. This is easily seen by noticing that the leaves of the trees and the flags stop their agitation as soon as the sun sets and resume it as soon as it rises. This nocturnal cooling is limited to altitudes of about 100 metres above the ground, since daytime heat exchange, dominated by convection, no longer exists. Thus an inversion layer is formed on the ground, where the temperature increases before returning to the normal values of the standard atmosphere (Figure 1b). As a result of morning warming by solar radiation, the temperature of the ground rises again, as well as that of the lower atmospheric layers. This can contribute to situations like the one in Figure 2, where the still very cold inversion layer is no longer located at ground contact but a few tens of metres higher. However, the orientation of the slopes adds another contribution, with those oriented to the southeast warming faster than the valley bottom.

During the coldest seasons, from November to March in the northern hemisphere, in this resting air, the dew point [2] can be reached close to the ground. The water vapour initially present in the air can therefore condense overnight and form mists and fogs consisting of aerosols [3] too small to fall. At sunrise, as the ground heats up, the lower layers of air become lighter and rise by lifting these aerosols and compressing the layers above them. This compression leads both to heating [4] which amplifies this temperature inversion and to a kind of compression which can transform the fog layer that may be present and just lifted into a true stratus cloud (Figure 3). Gradually, at the beginning of the day, this layer, which absorbs a significant part of the solar radiation, heats up in turn, droplets evaporate and the fog can disappear completely. In winter, as long as anticyclonic conditions last, this is often not the case at northern European latitudes and fog and the inversion layer often persist for several days.

3. The fogs

The droplets present in fogs are in fact assemblages of water molecules in very large numbers around solid particles often smaller than a micron in size. Globally this object with a solid fraction and a liquid fraction is called a hydrometeor. The conditions of its formation are described in the article What’s happening in the clouds? Just like fine particles suspended in dry air (Read: Air Polluting Particles: What are they?), especially PM10 and PM2.5, many hydrometeors are so small that they cannot fall out. However, it should be noted that a hydrometeor with an average radius of a few microns could contain about a billion water molecules about a nanometre apart.

This maintenance of equilibrium of an object whose density is 1000 times greater than that of the surrounding air can be explained as follows. Two forces must be compared: the weight of this object, which would be the engine of its fall, and the friction of the air initially located below, which would rise to take the place of this hydrometeor and which would constitute the antagonistic force. The weight is proportional to the cube of the average radius (r³) of the object. The friction is proportional to the outer surface of the object, i.e. the square of the mean radius (r²). When this radius becomes very small, the weight becomes negligible compared to the friction and the hydrometeors cannot fall. On the other hand, for raindrops, snowflakes and hailstones, whose size is larger than the balance between weight and friction, greater than about twenty microns, the balance is broken in favour of weight and these objects fall. The heaviest objects fall more quickly than those whose radius is close to that corresponding to the equilibrium, which gives rise to modest drizzle.

It should be added that when the fog layer is formed, its highest parts are subjected to fairly intense cooling by infrared radiation. Like the radiation from the ground, this contributes to the cooling of the entire layer. And the combination of these phenomena can lead to a strengthening of the temperature inversion, but also to a thickening of the inversion layer.

Pollutants of all kinds, whether they are of industrial origin such as smoke laden with carbon oxides and soot, nitrogen oxides, methane, ozone, or of natural origin such as pollens (Read: Air pollution), gather below this inversion layer or in its lower part (Figure 4). Like the hydrometeors in fogs, they stagnate without convective movement or turbulence. It is they that give these slicks a colour that may appear greyish, bluish or yellowish, depending on the nature of the pollutants. This colour results from the diffusion of light by these objects whose size is much larger than the wavelength, as required by Mie’s Law of Scattering [5] explained in the paper The colours of the sky. One of the best known special cases is the Vosges blue line [6], due to the presence of molecules secreted and expelled by trees, especially conifers, such as isoprene or sabinene.

During the coldest seasons, above a body of water, such as a fairly calm lake or river, a layer of mist is often present, as if it were deposited on the water. Remarkably, it does not disappear as quickly as the layer formed above the surrounding soil or vegetation. This delay in the disappearance of fog from lakes is due to the fact that the water surface reflects the first rays of the sun much better than neighbouring land. As a result, it does not heat up as quickly and can retain a relatively cold fog layer for a longer period of time where evaporation is delayed. In France, this situation is often observed in the Saône valley and on most lakes and ponds during the winter period.

4. The inversion layer of mountain valleys

Between December and March, in the presence of a winter high pressure, it is frequent that, for several days, the air temperature at the bottom of the Alpine or Pyrenean valleys remains lower than its value at altitude. It can even freeze in the valley under a persistent foggy layer, while above 1000 or 1500 m and under a beautiful sunny midday sun, thermometers indicate temperatures high enough to allow skiers and hikers to picnic in the open air (Figure 5).

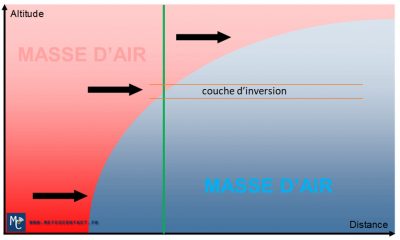
This anomaly is due to descents of cold and therefore heavy air from the vicinity of the peaks to the valleys. These cold air currents are called katabatic winds. Walkers can feel them quite clearly when they cross a combe where a torrent is flowing; locally they can be caught by this rather localized cold current which, like the water in the torrent, flows down towards the valley bottom. At the highest altitudes the snow cover reflects the sun’s rays very well and keeps the air at ground level at a fairly low temperature, often below 0°C. The katabatic wind is thus maintained at all hours of the day. These conditions are favourable for dew point, condensation of water vapour and the formation of a layer of fog at intermediate altitudes, between 500 and 1500 m. Hikers at higher elevations can then see this sea of cloud from above, from which the summits emerge (Figure 5), which may not disappear for several days. This cloud layer of varying thickness is the inversion layer where the temperature increases instead of decreasing as predicted by the standard atmosphere.

In the summer, well-cleared alpine pastures, forests and rocky slopes absorb the energy of the sun’s rays much better than in winter. In their vicinity and especially on the sunny slopes, from early morning, the air warms up, becomes lighter and forms the upward drafts that paragliders seek and which suck in the air from the vicinity. In the valleys too, the sunshine has warmed the air and allowed a certain agitation of this air. Towards midday, the morning katabatic wind that may be present on the slopes is then replaced by an updraft, called anabatic wind, which is much less localized in the combes than the katabatic wind. Its main effect, combined with the turbulent agitation that reappears with the day, is to renew the air in the valley, cooled during the night, and prevent the formation of an inversion layer.

The slopes of the mountain massifs that surround a valley have different orientations, which implies different schedules for the alternation between the morning katabatic wind and the later anabatic wind. On the other hand, these slopes can be gentler on one side and steeper on the other. When the valley widens, this can give rise to horizontal winds that have neither the same direction nor the same speed, and which can be located in layers one above the other. This can result in some stratification of the air in these valleys (Read: Stratification and Instability in Natural Fluid Environments).

5. Other examples of inversion layers

When a large mass of warm and generally humid air advances over a territory, its interface with the colder air initially present is called a warm front. Lighter than the cold air, the warm air passes over it, as shown in Figure 6. This front thus gives rise to an inversion layer that will accompany it during its advance and until it is destroyed. This is called a frontal inversion layer.

The tropopause, located above the troposphere at an altitude of about 12 km, is a very special inversion layer, characterized by a halt in temperature decline before further growth in the stratosphere. It is a transition zone between the troposphere, dense enough to be subject to upward heat transport by convective motions, and the stratosphere, where the air is too rarefied to transport heat well by convection. It is described in the article The Earth’s atmosphere and gas envelope. It is the absorption of ultraviolet radiation from the sun that becomes predominant in the stratosphere, where it causes chemical reactions that convert oxygen (O₂) into ozone (O₃) by releasing heat. As a result, the temperature rises again, from around -56°C in the tropopause to values close to 0°C at altitudes above 50 km.

6. Influence on sound and electromagnetic waves

Like many material media, the atmosphere has the property of allowing these two families of waves to propagate, although they result from profoundly different physical phenomena:

• the compressibility of air for sound waves that propagate with a velocity of about 340 m/s (Read: The Emission, Propagation and Perception of Sound),
• electric and magnetic field oscillations for electromagnetic waves that propagate at the speed of light of about 300,000 km/s (Read: The thermal radiation of the black body).

Nevertheless, both are sensitive to variations in air density and are attracted to the densest, i.e. coldest, regions. In periods of good weather, since the night-time cooling of air layers close to the ground makes them heavier, the paths of these waves are thus slightly curved towards the ground, giving them a significantly greater range in the early morning than in the middle of the day.

The physical property on which the wave path depends is the index of refraction, which varies like the density of air, which varies inversely with temperature but in the same direction as humidity. Thus, in France, when a warm, dry air mass, coming for example from the Sahara, passes over a cold, humid air mass, coming rather from the Mediterranean, the air density and the refractive index of the waves locally undergo particularly large variations. In such a situation the paths of both sound waves and electromagnetic waves are inclined towards the ground, giving them a curvature of the same sign as that of the earth. But there ends the analogy between these two families of waves, which have extremely different ranges: a hundred meters for sound, kilometers for light, hundreds or thousands of kilometers for hertzian waves, especially radar beams [7].

In resting air, sound waves propagate in all directions from the transmitter, gradually losing their intensity. This gradual weakening is due to the dissipation of their energy by the viscosity of the air and the distribution of this energy over an increasingly larger space as they propagate. When an inversion layer is present close to the ground, as it rises upwards the sound gradually passes through layers of increasingly hot air, whose density is lower and lower. This causes a refraction that bends the path of these waves to the horizontal. If the inversion is very pronounced, the sound waves initially propagating upwards are returned to horizontal directions, where they converge with those emitted horizontally. This concentration of energy increases the range of these sound waves in the horizontal directions, despite their progressive dissipation by the viscosity of the air. Thus, in the presence of an inversion layer above the ground, the human voice carries farther than in its absence.

Electromagnetic waves cover an extremely wide range of wavelengths, about 10^-12 m for gamma rays, 10^-9 m for X-rays, fractions of a micron (10^-6 m) for light, and tens or hundreds of metres for radio and radar. Radar waves are much better directed than sound waves because they are emitted by specially designed systems such as the beam shown in Figure 7. Often these transmitters are located at a fairly high altitude above the ground, at the top of a tower which may itself be placed at the top of a building, hill or high mountain.

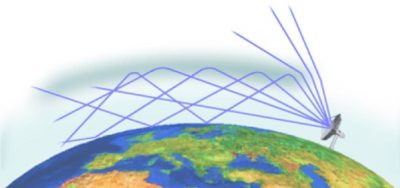
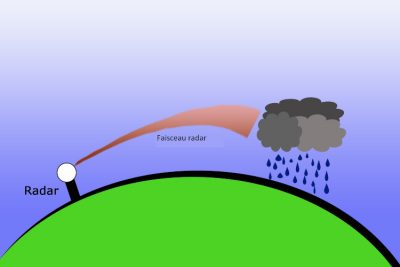
The electromagnetic waves of the radars thus form relatively channelled beams around their main direction and aim to detect distant objects thanks to the echoes they reverberate. This does not prevent them from undergoing refraction in the presence of an inversion layer. The diagram in Figure 7 shows that the inversion layer causes a curvature of the beam, which makes it possible to detect precipitation beyond the horizon. When it is very close to the globe, this beam curvature can lead to a waveguide effect [8]. This effect is particularly noticeable when the inversion layer is located at a fairly high altitude, between 500 m and 1500 m. Then, refracted downwards by the inversion layer and reflected upwards by the ground, the very well guided electromagnetic waves manage to propagate over very large distances (Figure 8).

7. The special case of light

This refraction phenomenon also applies to light, the visible band of electromagnetic radiation, whose wavelengths are between 0.4 and 0.8 microns. It is this phenomenon that makes the green ray visible, a rare optical phenomenon at sunset. This phenomenon makes it possible to notice a very small, flattened green spot on the horizon, visible only for a few seconds, just above the disappearing sun, propagated to the distant observer by the last rays of light that graze the horizon (Figure 9).

This green ray is the result of the combination of two different physical phenomena, which results in the elimination of other colours, or wavelengths, from the visible band.

When the Sun is about to disappear on the horizon, the red part of its radiation (wavelengths above 0.6 microns) is less refracted towards the ground than the green and blue parts (wavelengths below 0.5 microns), so that the red rays no longer reach the very distant observer. On the contrary, the blue and green rays emitted by the Sun follow the curvature of the Earth’s globe better because of their better refraction. On the other hand, Rayleigh Scattering (Read: The Colours of the Sky) has the effect of distributing the blue part of the spectrum in all directions, which attenuates the fraction of blue rays coming directly from the Sun and directed towards the observer. As a result, very ephemerally and rarely, in the last few seconds before nightfall, a narrow band of light with a wavelength close to 0.55 microns, which corresponds to the colour green, may still reach the distant observer.

The formation of superior mirages [9], i.e. images of an object visible at a higher altitude than its own, is another illustration of this phenomenon of refraction in an inversion layer located near the ground. For this reason these mirages are often called cold mirages. The fact that, from Nice, at dawn, one can observe the mountains of Corsica while their highest peak, Monte Cinto, is located below the Nice horizon is another illustration of this refraction phenomenon that forces light rays to follow the curvature of the globe (Figure 10). This image disappears as soon as the inversion layer disappears due to daytime heating. Other examples of cold mirages have been the subject of stories, even legends [10], such as the ghost ship painted by Charles Temple Dix around 1860 (Figure 11). This refraction of light in an inversion layer located on cold ground can be observed on the ice pack or on the Antarctic continent.

8. Messages to remember

• It is the cooling of the ground, either during the night or following a descent of fresh air from the heights by katabatic wind, which imposes a lower temperature than that of the standard atmosphere just above the ground or water bodies. The inversion layer is located below the altitude at which the air temperature returns to its linear decay consistent with the standard atmosphere.
• In winter, this cooling can cause the lower atmosphere to pass the dew point and be subjected to condensation of the water vapour initially present, resulting in the formation of fogs.
• Heavier in the lower part than in the upper part of an inversion layer, the air is very stable and free of convective motion and turbulence. It then behaves like a cover that prevents the renewal of air and the evacuation of pollutants.
• An inversion layer can also appear at an intermediate altitude when a warm front arrives and passes over an already present cold air mass. It is called a frontal inversion layer.
• These inversion layers have the remarkable property of allowing sound and electromagnetic waves to be well channelled, thus increasing their range. The rare and ephemeral green ray and cold mirages are curious illustrations of this.

Thanks to Roland Blanpain, former Head of the Systems Division of CEA-LETI, and Christophe Delaveaud, Head of the Laboratory Antenna Propagation and Inductive Coupling of CEA-LETI-DSYS, as well as to Joël Sommeria, Director of LEGI, and Philippe Bougeault, former Director of CNRM, for proofreading this article and for their comments.

---

Notes and References

Cover image. Inversion layer and fog in mid-mountain [Source: © DivertiCimes]

[1] This linear decrease is, however, limited to the troposphere, because above 12,000 m in the stratosphere, other mechanisms come into play, such as the absorption of UV energy, which causes a further increase in temperature.

[2] The dew point is the temperature at which the air must be cooled so that the water vapour it contains condenses into dew or frost. At any temperature, there is a maximum amount of water vapour that air can hold, called the water vapour saturation pressure. Any additional water is condensed into droplets where excess water molecules collect.

[3] An aerosol is an assembly of fine solid particles, or liquid droplets, or an assembly of both, suspended in a gaseous medium. Typical examples are droplets suspended in mists or fogs.

[4] Any gas under compression also experiences a temperature rise. This is because pressure and temperature are magnitudes that express on macroscopic scales the consequences of one and the same phenomenon: molecular agitation (Read: Pressure, temperature and heat). A well-known example is the heating of bicycle pumps during compression is a well known example.

[5] Gustav Mie, Beiträge zur Optik trüben Medien, speziell koloidaller Metallösungen, Annalen der Physik, Leipzig, vol. 25, 1908, pp. 377-445

[6] This expression “the blue line of the Vosges” was coined by Jules Ferry, who used it in 1893 in his will. But the physical phenomenon that explains it is not peculiar to the Vosges.

[7] The word radar is an acronym for Radio Detection And Ranging. It refers to systems that use electromagnetic waves to detect the presence and velocity of distant objects that return a signal similar to the echo of sound waves back to the transmitter. The distance is proportional to the duration of the signal’s round trip.

[8] A waveguide is a system designed to channel electromagnetic waves into a particular medium, such as an optical fibre, to avoid their dispersion and thus make their path as long as possible. In general, this process relies on refractive index variations between different media to bring the divergent rays back to the channel.

[9] In contrast, lower mirages, or hot mirages, are those due to the presence of a layer of particularly hot air on the ground, for example in deserts or on very sunny roads, which allows one to see images of objects located above this layer.

[10] John MacDonald, Travels in various part of Europe, Asia and Africa during a serie of thirty years and upward, Forbes, 1790.